今回は、行列演算では基礎として習う行列式を求めるnp.linalg.det関数を解説します。

行列式

まずは線形代数で扱う行列式についておさらいしておきましょう。

行列式は一般的には以下の形で記述されることが多いです。

|A| \\ detA \\

行列式は、一般にある線形方程式を行列を使って解くときなどに非常に効力を発揮します。一般公式は非常に複雑ですので、2×2と3×3の行列の行列式の求め方を示します。

A\ \ = \ \left( \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{array} \right )

とすると、

|A| \ \ = \ a_{11}a_{22} - a_{12}a_{21}

のようにして行列式を求めることができます。ちょうど、対角成分の掛け合わせを差し引くと求められます。

次に3次元の行列式の場合の求め方です。ここまで分かっていればあとは様々な定理を使うことで4次以上の行列の行列式を求めることも可能になります。(この辺りは線形代数の入門書に載っている内容ですのでそちらを参照してください)

A\ \ = \ \left( \begin{array}{cc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{array} \right )

とすると、

|A| \ \ = \ \ a_{11}a_{22}a_{33}\ + \ a_{12}a_{23}a_{31}\ +\ a_{13}a_{21}a_{32}\ - \ a_{11}a_{23}a_{32}\ -a_{12}a_{21}a_{33}\ - \ a_{13}a_{22}a_{31} \\

式だけだと少しわかりにくいので、簡単な図にすると以下のようになります。

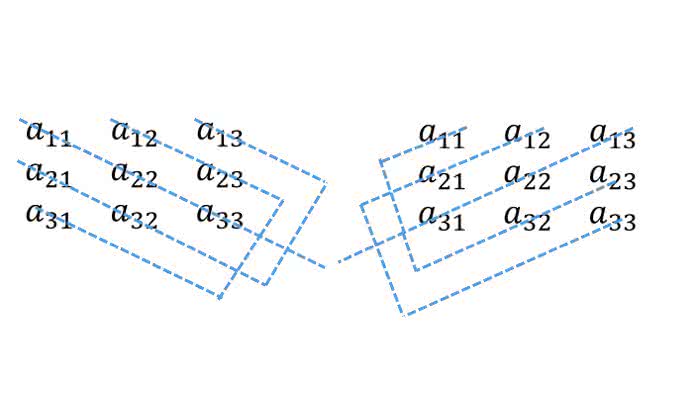
左側が足し合わせる要素で、右側が差し引く要素の組み合わせとなっています。 上の式と照らし合わせてみると、この図が意味していることがわかりやすいかと思います。

詳しい解説は以下のサイトを参考にしてみてください。

・行列式の３つの定義と意味 –高校数学の美しい物語–
・行列式 -Yokota Lab

numpy.linalg.det()

では早速関数自体の使い方についてみていきましょう。

APIドキュメント

np.linalg.det()関数のAPIドキュメントは以下の通りです。

numpy.linalg.det(a)

args:

パラメータ名 型 概要
a shape=(….,M,M)となっているような配列 行列式を求めたい行列（配列）を指定します。

returns:

行列式が返されます。

引数として指定できるのは行列式を求めたい行列のみです。返ってくる値も、それぞれの行列に対応した行列式となります。

サンプルコード

早速使い方をみていきましょう。linalgモジュールはLAとしてimportするのが慣例なので、ここでもそれに倣います。

In [1]: import numpy as np

In [2]: import numpy.linalg as LA # linalgモジュールはLAとしてimportするのが慣例。

In [3]: a = np.array([[2,3],[4, -1]])

In [4]: a
Out[4]:
array([[ 2,  3],
       [ 4, -1]])

In [5]: LA.det(a) # aの行列式を求める。
Out[5]: -14.000000000000004

In [6]: b = np.array([[1,1], [2,2]]) # 行列式が0になるものを持ってくる。

In [7]: b
Out[7]:
array([[1, 1],
       [2, 2]])

In [8]: LA.det(b)
Out[8]: 0.0

要素が複素数となっても対応できます。

In [9]: c = np.array([[1-1j, 3j],[-3j, 1+2j]]) # 要素が複素数でも問題ない。

In [10]: c
Out[10]:
array([[ 1.-1.j,  0.+3.j],
       [-0.-3.j,  1.+2.j]])

In [11]: LA.det(c)
Out[11]: (-6.0000000000000009+1j)

では次は３次元の行列についても扱っていきましょう。

In [12]: d = np.random.randint(-5, 6, size=(3,3,3))

In [13]: d
Out[13]:
array([[[-2,  4,  5],
        [-4, -4,  2],
        [ 4, -1, -1]],

       [[ 0, -3, -4],
        [-5, -1, -2],
        [ 1,  4, -2]],

       [[-2,  0,  4],
        [-3,  2,  0],
        [ 4, -2, -4]]])

In [14]: LA.det(d)
Out[14]: array([ 104.,  112.,    8.])

このように、３次元においては複数の行列に対して行列式を求めるかたちとなっています。

参考

*numpy.linalg.det — NumPy v1.13 Manual
*行列式の３つの定義と意味 –高校数学の美しい物語–
*行列式 -Yokota Lab