NumPyは、多次元配列を基本的なデータ構造として操作するライブラリです。そのため、NumPyにはPythonのリストを使った演算ではなく、効率性などからndarrayという独自のデータ構造を使います。
NumPyを勉強するにあたって、ndarrayについて知っておくことでコードの高速化やメモリの省メモリを意識したコードを書くことができるようになります。
一般に、NumPyは科学技術計算のためにつくられたライブラリということもあって、大量のデータや高速に演算したいことは多いはずです。
今回は、基礎の基礎となる部分である、ndarrayについて一から解説したいと思います。他の記事では、ndarrayのことを配列と日本語で表記することが多いですが基本的に両者は同じものを指しています。
ndarray
定義
まずは公式サイトにのっているndarrayの定義からみていきましょう。公式サイトには以下のように書いてあります。
An ndarray is a (usually fixed-size) multidimensional container of items of the same type and size.
これを日本語で直訳してみると、次のようになります。
ndarrayはたいてい一定の大きさを持つ、同じサイズや型で構成された複数要素の多次元の容れ物である。
ざっくり言うと、同じ属性や大きさを持った要素を持つ多次元配列を扱うためのクラスの1つということです。そもそもndarrayというのはN-dimensional arrayの略となっており、N次元配列を略しただけですね。
この同じ属性や大きさを持った要素の部分は意外と重要です。これはndarrayインスタンスの中に格納される要素は全て同じ種類のデータ型やサイズでないといけないことを意味します。
Pythonのリストのように要素ごとにデータ型を柔軟に変えることはできず、サイズも可変ではありません。
このクラスndarrayの特徴は以下の通りです。
- 同じ型を持つ要素しか格納することができない
- 各次元ごとの(2次元なら列ごとや行ごと)の要素数は必ず一定
- C言語を元に、最適化された行列演算を行うため効率的な処理をすることができる
ndarrayにすることで、多次元データを扱うための便利な属性を使用することができるようになります。
属性(attributes)
ここではndarrayが持つ属性を紹介していきます。(インスタンス変数名).(属性)とすればインスタンスとなっているndarrayの情報を取得することができます。
| 属性 | 説明 |
|---|---|
T |
いわゆる転置を返す。ndim(後述)<2のときは元の配列が返される。 |
data |
配列のデータがどこから始まっているのかを示すPythonのバッファーオブジェクト。 |
dtype |
ndarrayに含まれる要素が持つデータ型。 |
flags |
メモリ上におけるndarrayのデータの格納の仕方(Memory Layout)についての情報。 |
flat |
ndarrayを1次元配列に変換するイテレーター。 |
imag |
ndarrayにおける虚数部分(imaginary part)。 |
real |
ndarrayにおける実数部分(real part)。 |
size |
ndarrayに含まれる要素の数。 |
itemsize |
バイト単位での一つ一つの要素の大きさ。 |
nbytes |
そのndarrayの要素によって占められるバイト単位でのメモリ総量。 |
ndim |
ndarrayに含まれる次元の数。 |
shape |
ndarrayの形状(shape)をタプルで表したもの。 |
strides |
各次元方向に1つ隣の要素に移動するために必要なバイト数をタプルで表示したもの。 |
ctypes |
ctypesモジュールで扱うためのイテレーター。 |
base |
ndarrayのベースとなるオブジェクト(どのメモリを参照しているのか)。 |
情報にアクセスしても配列(ndarray)の中身や情報は一切変わることはありません。例えば、.Tで転置させたものを表示させたとしても元のデータが変更になることはありません。
T,data,dtype
属性がどのように表示されるのか、実際のコードでみていきましょう。まずはTやdata、dtypeについてです。dataはPythonのバッファーオブジェクトで、どこから配列のデータが始まっているのかを示しています。dtypeはndarrayのデータ型になります。
転置とdtypeについては以下の記事で詳しく解説しているので参考にしてみてください。
配列の軸の順番を入れ替えるNumPyのtranspose関数の使い方 - DeepAge /features/numpy-transpose.html
NumPyにおける要素のデータ型dtypeの種類と指定方法 - DeepAge /features/numpy-dtype.html
In [1]: import numpy as np # NumPyモジュールをインポート
In [2]: a = np.array([1,2,3]) # ndarrayインスタンスを生成。
In [3]: type(a) # クラスを確認
Out[3]: numpy.ndarray
In [4]: b = np.array([[1,2,3], [4,5,6]]) # これで2-dimensional array(2次元配列)
In [5]: a
Out[5]: array([1, 2, 3])
In [6]: b # 各々表示させるとこんな感じ。
Out[6]:
array([[1, 2, 3],
[4, 5, 6]])
In [7]: b.T # 転置
Out[7]:
array([[1, 4],
[2, 5],
[3, 6]])
In [8]: a.T # a.ndim < 2なので変化なし。
Out[8]: array([1, 2, 3])
In [9]: a.data # メモリの位置を示す。
Out[9]: <memory at 0x106f54888>
In [10]: a.dtype # データ型
Out[10]: dtype('int64')flags,flat
次は、メモリレイアウトについての情報を表示させる.flagsと、1次元配列へと変換するイテレーターとなる.flatです。.flat[n]で、ndarrayを1次元に変換した際にn番目にくる要素を表示します。
In [11]: a.flags
Out[11]:
C_CONTIGUOUS : True
F_CONTIGUOUS : True
OWNDATA : True
WRITEABLE : True
ALIGNED : True
WRITEBACKIFCOPY : False
In [12]: b.flags # いろんな情報が表示される。
Out[12]:
C_CONTIGUOUS : True
F_CONTIGUOUS : False
OWNDATA : True
WRITEABLE : True
ALIGNED : True
WRITEBACKIFCOPY : False
In [13]: a.flat[1] # aを1次元配列にしたときのn番目の要素を表示。
Out[13]: 2
In [14]: b.flat[4] # bを1次元配列にしたときの4番目の要素を表示。
Out[14]: 5real,imag
次は複素数(complex)の要素に対してself.realとself.imagを使って実部と虚部を表示させます。
In [15]: c = np.array([1.-2.6j, 2.1+3.J, 4.-3.2j]) # 複素数を要素とするndarrayインスタンスを生成
In [16]: c.real # 実部
Out[16]: array([ 1. , 2.1, 4. ])
In [17]: c.imag # 虚部
Out[17]: array([-2.6, 3. , -3.2])size,itemsize,nbytes
次は要素の数を表示する.sizeと、バイトオーダーでの要素1つ1つがメモリで占める容量を表示する.itemsize、これらの積となっており配列の要素全ての容量を表示する.nbytesです。
In [18]: a.size # 要素の数
Out[18]: 3
In [19]: b.size # 環境によっては4になる
Out[19]: 6
In [20]: a.itemsize # バイトオーダーでの要素1つ1つの長さ
Out[20]: 8
In [21]: b.itemsize
Out[21]: 8
In [22]: c.size, c.itemsize # cの方がsizeにたいしてitemsizeが大きくなる。
Out[22]: (3, 16)
In [23]: a.nbytes # バイトオーダーでの配列の長さ 環境によっては12になる
Out[23]: 24
In [24]: b.nbytes # 環境によっては24になる
Out[24]: 48
In [25]: c.nbytes
Out[25]: 48
In [26]: a.size * a.itemsize == a.nbytes # この等式が成り立つ
Out[26]: Truendim,shape
次は次元数や形状(shape)について表示させる.ndimと.shapeについてです。次元や、shapeについては以下の記事で詳しく解説しているのでこれらの値が詳しくは何を意味しているのかについてはこれらの記事を参照してください。
NumPyの軸(axis)と次元数(ndim)とは何を意味するのか /features/numpy-axis.html
NumPyのndarrayのインスタンス変数shapeの意味 /features/numpy-shape.html
In [27]: a.ndim # 次元数
Out[27]: 1
In [28]: b.ndim
Out[28]: 2
In [29]: a.shape # 形状
Out[29]: (3,)
In [30]: b.shape # 形状
Out[30]: (2, 3)strides
次は.stridesです。このプロパティは各次元方向に1つ要素を移動するためにはメモリ場で何バイト動く必要があるのかを示したものです。詳しくはMemory Layoutの部分で解説します。
In [31]: d = np.array([[[2,3,2],[2,2,2]],[[4,3,2],[5,7,1]]]) # 3次元配列を生成
In [32]: d.shape, d.ndim # 形状を次元数を表示
Out[32]: ((2, 2, 3), 3)
In [33]: a.strides # 各次元方向(axis=ndim, axis=ndim-1,...,axis=1, axis=0)における1つの要素に移動するためのバイトオーダーでの距離 環境によっては(4,)となる
Out[32]: (8,)
In [34]: b.strides # .ndim = 2 環境によっては(12, 4)となる
Out[34]: (24, 8)
In [35]: c.strides # .ndim = 3
Out[35]: (16,)
In [36]: d.strides # .ndim = 3 環境によっては(24, 12, 4)となる
Out[36]: (48, 24, 8)ctypes,base
次は.ctypesと.baseです。.ctypesはctypesモジュールを使った操作を行うためのイテレータとなります。.baseはこの配列がビューであるならビューをしている元の配列を示します。
コピーとビューに関しては、以下の記事を参考にしてください。
NumPyのコピー(copy)とビュー(view)を分かりやすく解説 /features/numpy-copyview.html
In [37]: a.ctypes.data # ctypesモジュールを使った操作
Out[37]: 140421253863024
In [38]: a.base # aのベースとなる配列はどこか。
In [40]: e = a[:2]
In [41]: e.base
Out[41]: array([1, 2, 3])
In [42]: e.base is a
Out[42]: True
In [43]: a.base is e.base
Out[43]: FalseMemory Layout
NumPyにおける行列計算のパフォーマンスをより向上させるためにはメモリ上でndarrayの要素がどのように格納されているかを知る必要があります。内部メモリーでどのように配列が保存されているかを意識しておくだけで、随分と理解が進みます。
クラスndarrayで生成されたインスタンスはメモリ上では1次元で保存されます。ここに登録される情報で、データ型や形状(shape)といった1次元で並べられた要素のデータの読み取り方を指定した部分をメタデータと呼びます。
このメタデータに続き、要素をデータ化したものが並んでいきます。データの格納の仕方は大きく分けて2つ存在します。
1つはローメジャー(row-major)オーダーでもう1つはカラムメジャー(column-major)オーダーです。前者はC言語で使われている並べ方で、後者はフォートランやMatlabで使われている並べ方です。
先ほど紹介した属性で.flagsというものがありましたが、その中に次のような部分がありました。
C_CONTIGUOUS : True
F_CONTIGUOUS : FalseこのC_CONTIGUOUSというのがローメジャーで読み込むことが可能かどうかといったもので、F_CONTIGUOUSがカラムメジャーで読み込むことが可能かどうかを示しています。よくNumPyの引数でorderというものがありますが、基本的には'C'とするとローメジャーに、Fとするとカラムメジャーでデータが格納されていきます。
この2つの違いはどの次元方向からデータを格納していくかにあります。ローメジャーでは高い次元から(axisの番号が若い順)格納していき、カラムメジャーでは低い次元(axisの番号が高い順)から格納していきます。
2次元配列の例で詳しく解説してみます。例えば、以下のような2×3の2次元配列があったとします。
2次元でいくとローメジャー(order=’C’)では行方向から順に要素が格納されていきます。
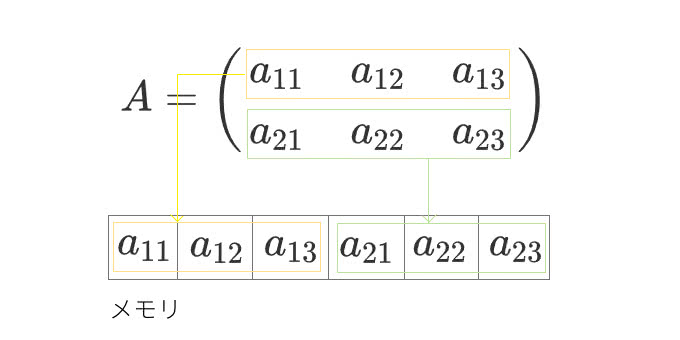
一方でカラムメジャー(order=’F’)では列方向から順に要素が格納されていきます。
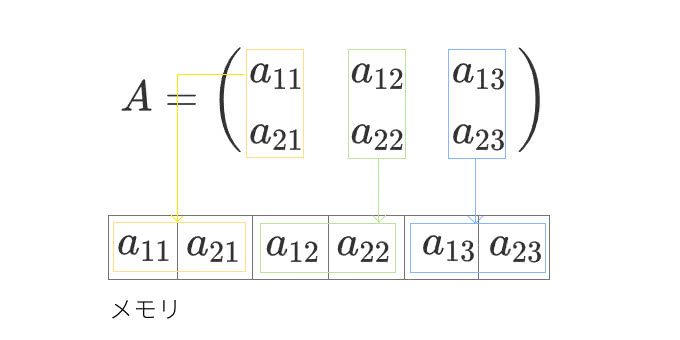
列方向は2次元においてはaxis=0、行方向はaxis=1となり、軸の番号は変わりはするものの同じ大小関係が成り立ちます。このように配列のデータはメモリ上に格納されています。
ストライド
列方向に処理を展開していきたい場合、ローメジャーの方が1つ1つの要素のメモリー上における距離が小さくてすみます。一方、カラムメジャーで同じ処理を行うと行方向に収納されているので列ごとに移動するためのバイト数が大きくなり、効率的に計算を行うことができません。
この1つ1つの要素にアクセスするためにメモリー上での移動距離をバイト数で表したものをストライド(strides)と呼びます。
これはndarrayの属性(attributes)の1つとなっており、この情報を見ることで要素の距離をつかむことができます。カラムメジャーとローメジャーでそれぞれ同じ配列を格納してみます。
In [82]: a = np.random.randn(100,100)
In [83]: b = np.array(a, order ='C') # row-major
In [84]: c = np.array(a, order ='F') # column-major
In [85]: b.strides, c.strides # ストライドを見ると、距離が逆転している。
Out[85]: ((800, 8), (8, 800))
In [87]: np.allclose(b, c) # 配列の要素が全部一致しているか確認
Out[87]: True次に、スライス表記を使って要素を100個飛ばしに読み込むように指定してみて計算速度の違いを確かめてみます。こうすることで、メモリー上の値を読み込む時、隣の要素を読み込むためにジャンプする必要のあるバイト数が増えるため計算速度が低下してしまいます。
In [48]: x = np.ones((100000,))
In [53]: y = np.ones((100000*100,))[::100] # 100個飛ばしに読み込む
In [54]: x.strides # 1つ隣の要素にたどり着くために8バイト分ジャンプするだけでいい。
Out[54]: (8,)
In [55]: y.strides # 1つ隣の要素にたどり着くために800バイト分ジャンプする必要がある。
Out[55]: (800,)
In [56]: x.shape, y.shape
Out[56]: ((100000,), (100000,))
In [57]: %timeit x.sum() # こちらの方が断然早い
51.9 µs ± 2.28 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)
In [58]: %timeit y.sum()
1.24 ms ± 201 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)後に何度も計算する必要がある場合、速度の低下を防ぐためにはビューで計算するのではなく、コピーを作成して計算した方が速くなる時ときがあります。
In [91]: y_copy = np.copy(np.ones((100000*100,))[::100])
In [92]: y_copy.strides
Out[92]: (8,)
In [93]: %timeit y_copy.sum()
60.9 µs ± 16 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)ブロードキャスト
ndarrayの特徴として、ブロードキャストを使用できる点があります。ブロードキャストを使いこなすことで、コード量を格段に減らすことができるようになります。詳細は以下の記事を参考にしてください。
NumPyのブロードキャストのメリットと解説 - DeepAge /features/numpy-broadcasting.html
ブロードキャストは計算処理を行う際に、適宜配列を拡張してくれる便利な機能です。例えば、配列aの全要素に対して1を加算したいとき、
a += 1とするだけで全ての要素に対して1が加算されます。このときブロードキャストが適用されています(aの次元はいくつでも構いません)。2次元配列に対して1次元配列を足し合わせることも可能です。
In [94]: a = np.array([1,2,3])
In [95]: b = np.array([[1,1,1],[2,4,1]]) # 2次元配列
In [96]: b + a # ブロードキャスト適用
Out[96]:
array([[2, 3, 4],
[3, 6, 4]]) 人工知能の今と一歩先を発信するメディア
人工知能の今と一歩先を発信するメディア