NumPyのndarrayは多次元配列を扱うデータ構造で、多次元のデータ構造をより操作しやすくするために、スライシングという機能を備えています。
Pythonのリストは、以下のように特定の範囲を切り取ることができます。
In [1]: a = [1, 2, 3, 4, 5]
In [2]: a[1:-1]
Out[2]: [2, 3, 4]:を使って範囲の始めのインデックスと終わりのインデックスを指定することで、目的の要素を取得することができます。
NumPyのndarrayのスライシングは、同様の機能を多次元に拡張したようなものです。
スライシングとは
スライシングとは、配列の中において、特定の範囲の要素を抜き出す際に利用する機能です。この範囲に対して特定の値を代入することや切り取ることなどできます。NumPyのスライシングは使い勝手良いので使い方をマスターすれば、要素の抜き出しに困ることはないでしょう。
使い方
各々の軸(axis)方向において
各々の次元においてstart:stop:stepを指定します。それぞれの意味は、
start : 始点stop :終点step:いくつの要素ごとにみるか
です。例えば、ある次元においてk番目の要素からl番目の要素まで二個おきに抜き出したいときは、k:l+1:2とすれば目的の要素を抜き出すことができます。15の連番から5~10を2ステップごとに抜き出す例が以下になります。
In [1]: import numpy as np
In [2]: a = np.arange(15)
In [3]: a
Out[3]: array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14])
In [4]: a[5:11:2]
Out[4]: array([5, 7, 9])注意すべき点は、最初の要素は0番目になること(kとlはそのようにして数えました) と、stopに指定されたインデックスはスライシングの際に抜き出されない(範囲外)になることです。
また、逆順にすると-1から数え始めることになります。
インデックスの付け方についてまとめると、以下のようになります。
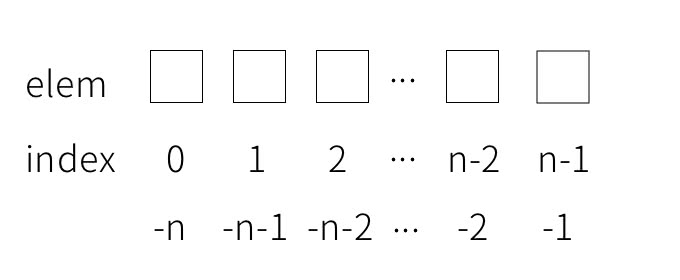
範囲が配列の最初から、または最後までといった場合はstart,stopに値を入れる必要はありません。
-
startを省略する場合は:stop:step -
stopを省略する場合は、start::step -
stepを省略する場合はstart:stop
となります。また、全範囲を選択したいときは:だけで十分です。
このstepの値を負の値にすると、逆順に何個置きに要素を見ていくかを指定できます。特に-1のときは全ての要素を逆順に並べなおすので小技としてよく使われます。
まずは、1次元配列で感覚をつかんでいきます。
In [1]: import numpy as np
In [2]: a = np.arange(10) # 10個の連番を要素とする配列で見てみる。
In [3]: a
Out[3]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
In [4]: a[1:5] # 1~4
Out[4]: array([1, 2, 3, 4])
In [5]: a[2:8:2] # 2~7を1個置きで
Out[5]: array([2, 4, 6])
In [6]: a[::-1] # これで逆順に
Out[6]: array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0])
In [7]: a[:3] # 0~2
Out[7]: array([0, 1, 2])
In [8]: a[4:] # 4~9
Out[8]: array([4, 5, 6, 7, 8, 9])
In [9]: a[:3],a[3:] # 3を境に2つに分割
Out[9]: (array([0, 1, 2]), array([3, 4, 5, 6, 7, 8, 9]))
In [10]: a[::2] # 2個おきで。
Out[10]: array([0, 2, 4, 6, 8])
In [11]: a[:] # 全範囲
Out[11]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])多次元への拡張
あとは、この各次元ごとのスライスを組み合わせていくだけです。軸(axis)の番号が若いものから順に指定していきます。次元ごとには[:,:,:]のようにカンマ,で区切ります。
axisについてよくわからないのであれば、以下の記事で詳しく解説していますので、参照してみてください。
NumPyの軸(axis)と次元数(ndim)とは何を意味するのか /features/numpy-axis.html
2次元配列から見ていきましょう。よくわからなくなってきたときは、次元の1つ1つを処理していきながら見ていくと何が起こっているか、見えやすくなるかと思います。
In [12]: b = np.arange(20).reshape(4,5) # 4×5の二次元配列
In [13]: b
Out[13]:
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]])
In [14]: b[1:3, 2:4] # 1~2行目、2~3列目を抜き出す
Out[14]:
array([[ 7, 8],
[12, 13]])
In [15]: b[:2, 1:] # 0~1行目、1~4列目を抜き出す
Out[15]:
array([[1, 2, 3, 4],
[6, 7, 8, 9]])
In [16]: b[::2, :] # 行方向に二個ごと
Out[16]:
array([[ 0, 1, 2, 3, 4],
[10, 11, 12, 13, 14]])
In [17]: b[:, ::2] # 列方向に二個ごと
Out[17]:
array([[ 0, 2, 4],
[ 5, 7, 9],
[10, 12, 14],
[15, 17, 19]])
In [18]: b[:, ::-1] # 逆順
Out[18]:
array([[ 4, 3, 2, 1, 0],
[ 9, 8, 7, 6, 5],
[14, 13, 12, 11, 10],
[19, 18, 17, 16, 15]])
In [19]: b[::-1, ::-1] # 全部ひっくり返す
Out[19]:
array([[19, 18, 17, 16, 15],
[14, 13, 12, 11, 10],
[ 9, 8, 7, 6, 5],
[ 4, 3, 2, 1, 0]])3次元配列をみていきます。値を代入していくことでどこを示しているのか分かりやすくしようと思います。難しそうに感じますが、2次元への拡張と同様に、3次元もただ2次元から1つ次元を増やしただけです。
In [22]: c = np.zeros((3,4,5)) # 3×4×5の3次元配列
In [23]: c
Out[23]:
array([[[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.]],
[[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.]],
[[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.]]])
In [24]: c[1:,1:4,:] = 1
In [25]: c
Out[25]:
array([[[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.]],
[[ 0., 0., 0., 0., 0.],
[ 1., 1., 1., 1., 1.],
[ 1., 1., 1., 1., 1.],
[ 1., 1., 1., 1., 1.]],
[[ 0., 0., 0., 0., 0.],
[ 1., 1., 1., 1., 1.],
[ 1., 1., 1., 1., 1.],
[ 1., 1., 1., 1., 1.]]])
In [26]: c = np.zeros((3,4,5)) # リセット
In [28]: c[:,1:2,3:] = 1
In [29]: c
Out[29]:
array([[[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 1., 1.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.]],
[[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 1., 1.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.]],
[[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 1., 1.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.]]])
In [31]: c = np.zeros((3,4,5)) # リセット
In [32]: c[:, :, ::2] = 1# 2個ごと
In [33]: c
Out[33]:
array([[[ 1., 0., 1., 0., 1.],
[ 1., 0., 1., 0., 1.],
[ 1., 0., 1., 0., 1.],
[ 1., 0., 1., 0., 1.]],
[[ 1., 0., 1., 0., 1.],
[ 1., 0., 1., 0., 1.],
[ 1., 0., 1., 0., 1.],
[ 1., 0., 1., 0., 1.]],
[[ 1., 0., 1., 0., 1.],
[ 1., 0., 1., 0., 1.],
[ 1., 0., 1., 0., 1.],
[ 1., 0., 1., 0., 1.]]])
In [34]: c = np.zeros((3,4,5)) # リセット
In [35]: c[::2, ::2, ::2] = 1
In [36]: c
Out[36]:
array([[[ 1., 0., 1., 0., 1.],
[ 0., 0., 0., 0., 0.],
[ 1., 0., 1., 0., 1.],
[ 0., 0., 0., 0., 0.]],
[[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.]],
[[ 1., 0., 1., 0., 1.],
[ 0., 0., 0., 0., 0.],
[ 1., 0., 1., 0., 1.],
[ 0., 0., 0., 0., 0.]]]) 人工知能の今と一歩先を発信するメディア
人工知能の今と一歩先を発信するメディア