様々な分野でビッグデータの応用が進んでいます。 その中でも企業が競争力を持つための、トレンド予測や需要予測が注目されています。
膨大なデータを解析することで、トレンドの変化や周期的な法則を導き将来を予測することができます。 今回は未来予測を目的としたデータの解析手法について紹介します。
この記事では以下を取り上げます。
-
ビッグデータとロングテール
-
解析手法「回帰分析」と「時系列分析」
-
時系列分析で注目を集めるSARIMAモデル
ビッグデータと未来予測
ビッグデータが広く認知される以前から、未来予測のためにデータを用いる取り組みは行われてきました。 ビジネス応用としてのデータ分析の関心ごとは、獲得したデータを分析し、いかに顧客行動を予測するかです。
そしてビッグデータが従来のデータと最も異なる点はデータの網羅性にあります。 つまり、データが母集団の一部のサンプリングではなく、母集団そのものを指すということです。
そしてこれはロングテールと呼ばれる情報を正しく活用した将来予測を可能にします。
ロングテールとは
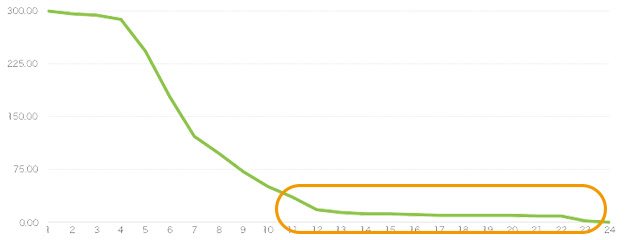
例えばあるECサービスに関して、商品を購入数順にソートし、横軸に商品、縦軸に購入数をとってグラフ化したとします。 上の図では左に行くほどたくさん購入された商品、右に行くほどあまり購入されていない商品ということになります。
左側に高く伸びる部分をヘッド、右側に細く伸びていく部分をテールと呼びます。 図では「多量な一部」と「少量な大部分」という構成になっています。 このようなデータは実世界では多く存在することが知られています。 これに即してテール部分が長く伸びるように現れるデータの性質を「ロングテール」と呼びます。
ビッグデータ分析では、このロングテールが重要なのです。 なぜ、このような出現の頻度が低い情報が重要視されるのでしょうか。
ロングテールとビッグデータの関連
ロングテールとビッグデータとはどのような関係があるのでしょうか。 前述のように、ビッグデータ以前のデータ解析では、基本的に扱うデータが母集団の一部分でした。
例えば数百から数万程度のサンプルデータを用いた商品の購買傾向の分析をおこなうとします。 その中で購買率が1%を切るような購買数が少ない商品は、該当するサンプル数が一桁であったり、場合によってはゼロとなってしまいます。 これでは統計的に意味のある分析を行うことが非常に難しくなってしまいます。
しかしこうしたロングテールに当たる商品についても、どのような傾向の人が購入しているのかを分析することは可能です。 その結果から似た傾向だがまだ購入していない顧客にレコメンドを送ることで、購買を促進することができます。
データからロングテールの部分に着目し、分析によって優れた洞察を得る。 これは今までは獲得することができなかった新たな価値です。 ロングテールはビッグデータだからこそ真価を発揮するということがご理解いただけたでしょうか。
未来予測のためのビッグデータ解析
将来予測のためのビッグデータ利用では、どのような分析手法が適切でしょうか。
現在は重回帰分析をはじめとする、回帰分析を用いた解析が一般的になっています。 そして、ビッグデータ時代ではSARIMAモデルなどの時系列分析にも注目が集まっています。
それぞれについて、詳しく説明していきます。
重回帰分析
重回帰分析は回帰分析の一手法です。 回帰分析はデータ系列間の関係性や影響力を調査し、そこから予測をおこなう手法です。
回帰分析には他にも単回帰分析と呼ばれるものがあります。
単回帰分析が1つの目的変数に対し1つの独立変数を用いて測するのに対して、 重回帰分析は1つの目的変数に対して複数の独立変数を用いて予測します。
回帰分析の基礎、単回帰分析
まず最もシンプルな単回帰分析について説明します。
単回帰分析は1つの予測したい変数に対して、影響を与える変数が1つである場合に用いる手法です。 この予測したい変数を目的変数、影響を与える変数を独立変数と呼びます。
目的変数をY、独立変数をXとすると、Y=aX+bという一次関数表すことができます。 もしaとbが分かれば、独立変数Xから目的変数Yを予測することが可能になります。
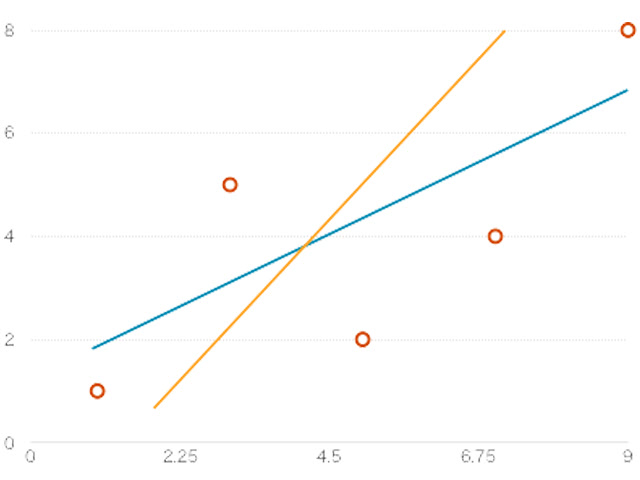
aとbはどのように求めればよいのでしょうか。 上の散布図を見てみましょう。 図のように一見正しそうな回帰直線は無数にあります。 この中から、最も予測誤差が少なくなるような直線を選択しなければなりません。 これを解決するため「最小二乗法」という手法が用いられます。
最小二乗法
最小二乗法は「データと回帰式の誤差の二乗和を最小にする」手法です。 少しわかりにくいので、図を用いて説明します。
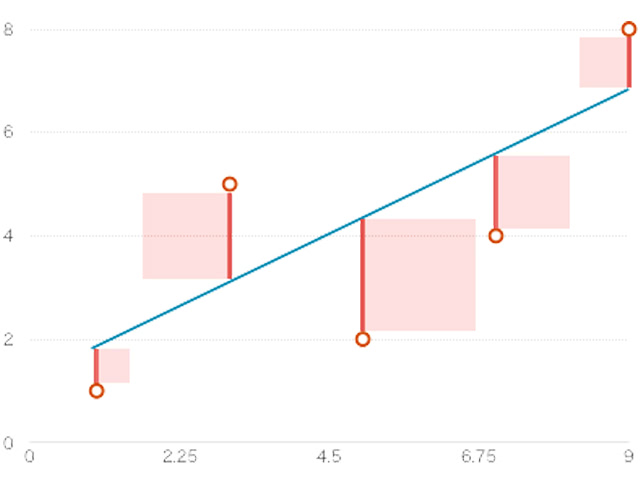
上図の赤線の長さが、データと回帰式との誤差にあたります。 「誤差の二乗和」は、赤い波線を一辺とした、正方形の面積の和になります。 つまりこの正方形の面積の和が最小になるようなaを求めます。
そして回帰直線は必ず(Xの平均、Yの平均)の点を通ることが知られています。 つまりaがわかっていれば、次の式よりbを求めることができます。
以上よりa、bから単回帰分析の回帰直線を求めることができます。
相関係数
単回帰分析で導いた一次方程式は、データにどれくらいばらつきがあるかによってその信用度が異なります。
その「信用度」を表す指標を相関係数と呼びます。 相関係数が高いほど、信用できる予測が可能になります。 点がばらけている場合は一次方程式で表すことが難しく、単回帰分析での相関係数は低くなります。
実世界のデータは複雑です。 単純な一次方程式で表すことのできるデータは非常に限られています。 実用的な面を考えると、もっと複雑な方程式で表現することが一般的でしょう。
重回帰分析
前述の通り、将来予測をする場合、1つの独立変数によって目的変数が決定することはほとんどありません。 実用的なケースでは重回帰分析が多く用いられます。
重回帰分析は1つの目的変数に対して複数の独立変数を用います。
変数の影響度
重回帰分析は複数の変数によって予測を行います。 1つの独立変数で表されるわけではないので、強い影響を与える変数もあれば、それほど影響を与えない変数も存在します。 そして目的変数と複数の独立変数の関係を分析したい場合、それぞれの独立変数がどれくらい影響を与えているかも大きな関心ごとの1つです。
そのようなどの独立変数がどれくらい目的変数に影響を与えるのかという指標を標準偏回帰係数と呼びます。 標準偏回帰係数を求めることで、目的変数を決定するための独立変数の関係を知ることができます。
多重共線性
重回帰分析で最も注意しなければならないのは、独立変数間の多重共線性です。
多重共線性とは、変数同士の相関関係を指します。 高い場合は変数間に強い相関があるということになります。
分析に用いる複数の独立変数が多重共線性を持つ場合、結果の誤差が大きくなります。 なぜならば、重回帰分析の独立変数はそれぞれが依存しない独立した変数であることが前提であるためです。
この多重線形性を確認するためには、独立変数間での相関係数を求めます。 相関係数が高い複数の独立変数は、どちらかを削除するなどの処理を施すことで、精度の向上が期待できます。
ビッグデータで重回帰分析を用いるリスク
ビッグデータを用いる場合、単純な重回帰分析ではうまく分析できないケースがあります。 変数の数が多くなることで、多重共線性を解消するのに非常にコストがかかるためです。
実用にたる分析をおこなう場合は、独立変数同士の多重共線性を確認し、 より高い精度が期待出来るデータを生成することが不可欠です。 データが増えるほど、多重共線性を網羅的に確認し適切な処理をおこなうことは難しくなります。
SARIMAモデル
将来予測における時系列分析に注目が集まっています。
時系列分析は過去の変数から目的変数を求める手法です。 そしてSARIMAモデルは、時系列分析の一手法です。
SARIMAモデルは複数の時系列モデルを複合した手法と考えることができます。 以下の図のような関係があります。
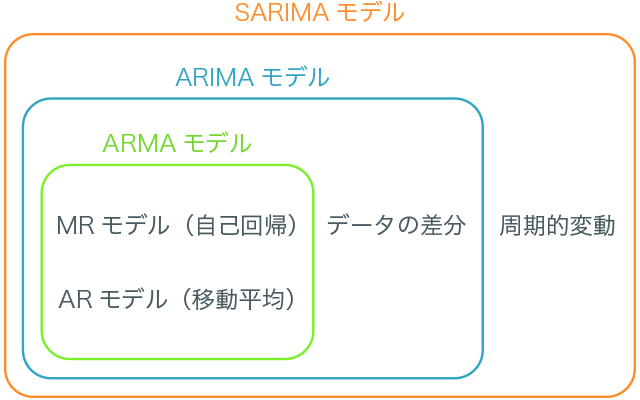
まずはARモデルとMAモデルについて説明していきます。
ARモデルとMAモデル
最も単純なモデルとして、ARモデルとMAモデルがあります。 ARモデルは自己回帰モデル、MAモデルは移動平均モデルとも呼ばれます。
ARモデル(自己回帰モデル)
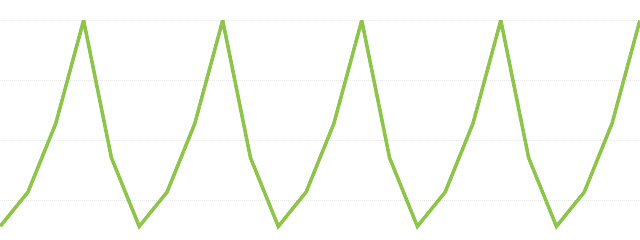
ARモデルは図のように時間の変化に対し規則的に値が変化する、最も単純な時系列モデルです。
直前のp個の値と相関のあるモデルをAR(p)と表現します。 ARモデルはある時点のデータがそれ以前のデータで回帰的に推定できるモデルです。
MAモデル(移動平均モデル)
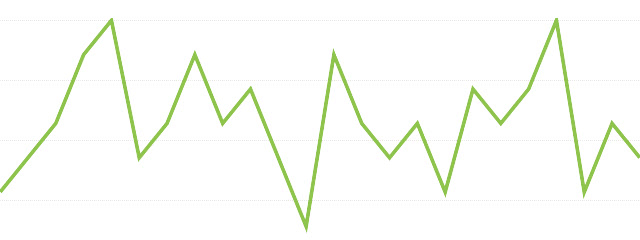
MAモデルは図のように時間の変化に対し不規則に値が変化します。 ただし、ある区間での変動が一定であるようにモデルを考えます。
直前のq個の値の誤差の影響を受けるモデルをMA(q)と表現します。
MAモデルは過去の誤差に影響されるモデルです。
ARMAモデル(自己回帰移動平均モデル)
ARモデルとMAモデルは競合する性質がほとんどないため、2つ組み合わせて定式化することができます。 これらを組み合わせたものが、ARMAモデルです。
ARモデルに関連する次数をpとMAモデルに関連する次数をqとすると、ARMA(p,q)と表すことができます。
ARMAモデルは過去の値から回帰的に推定可能な要素と過去の誤差に影響を受け、推定が難しい要素が組み合わさったモデルです。
定常過程と非定常過程
挙げて来たARモデル、MAモデル、ARMAモデルはいずれも定常過程を対象とした時系列モデルです。
定常過程は、以下の二つを満たします。
-
平均が時間に依存せずに一定である
-
異時点間の共分散が時間差のみに依存する
つまり、定常過程に従う時系列データは一定の周期で同程度の変動をしているということができます。
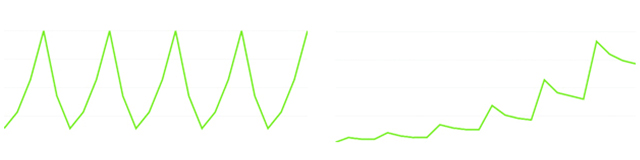
上の図を見てみましょう。 左のグラフはある区間で区切れば平均が一定に近いように思われますが、右側のグラフは明らかに増加傾向にあります。 つまり、一定の区間の平均を取った場合、その値が一定になることはありません。 したがって、右側のデータは定常過程ではありません。
このような定常過程ではない過程は非定常過程と呼ばれます。
時系列において、平均値が時間的に常に一定であることが保証されているのは稀です。 つまり現実に扱う時系列データは非定常過程であることが多いということになります。
実用に際しては、非定常過程の時系列データを対象とした手法を用いる必要があります。
ARIMAモデル(自己回帰和分移動平均モデル)
ARIMAモデルはARMAモデルを非定常過程に対応したものです。 研究用としては以前から用いられるモデルですが、2010年代頃からは実用化の流れも活発化しています。
ARIMAモデルはARMAモデルに加えて、前後のデータ間の差分dを定義します。
逆に言うと、非定常データから差分をとって定常データになるような値が差分dとなります。
このモデルはARIMA(p,d,q)と表すことができます。
SARIMAモデル(季節自己回帰和分移動平均モデル)
ARIMAモデルにさらに長期的な季節変動を取り入れたモデルが、SARIMAモデルです。
実際に存在する時系列データでは、季節の変動などがここに当たります。 季節的な変動もまた、異なるモデルで表されます。
ARモデルとMAモデルは短期的なモデル、ARIMAモデルの差分データやSARIMAモデルの季節変動は中長期的なモデルと考えることができます。 実際のデータではこれらの要素で綺麗に分解することのできる場合が多く見られるのです。
つまり、SARIMAモデルをまとめると以下のような形になります。
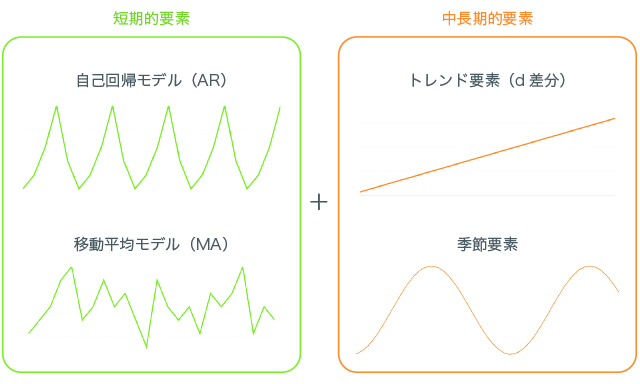
このように変動を表す成分を正しく分割して将来を予測することが、時系列分析の本質です。
まとめ
データと向き合い仮説を立てながら、様々なアプローチを試すことで適切な洞察に近づくことができます。 データを正しく表現することができる手法の選定は、データ自体の性質とデータを利用する目的によって様々です。
重回帰分析は需要の高い購買予測など様々な分野で広く用いられる手法であり、今後もその利用は進むでしょう。 時系列解析も流通などの分野ではすでに導入は進んでおり、今後もさらなる応用が期待されます。
そして、そのような専門性を持った人材であるデータサイエンティストの需要は高まっています。
ビッグデータの時代は、まだまだはじまったばかりです。 今後データ分析を正しく理解し、未来を見る眼を養うことはさらに重要になるでしょう。
 人工知能の今と一歩先を発信するメディア
人工知能の今と一歩先を発信するメディア



