今回は畳み込み積分(コンボリューション積分)を行ってくれる関数である、np.convolve関数について解説していきます。

畳み込み積分がよくわからないという方は、記事の後半の方で簡単に解説していますので、興味のある方はみてみてください。また、NumPyでは移動平均を求める際にもこの関数はよく用いられます。移動平均を求めることで、信号のノイズとかを消すこともある程度は可能になります。

np.convolve

まずは、convolve関数のAPIドキュメントを見て見ましょう。

numpy.convolve(a, v, mode = ‘full’)

params:

パラメータ名 型 概要
a array_like(長さN)
配列に相当するもの		 １番目の１次元配列
v array_like(長さM)
配列に相当するもの		 ２番目の１次元配列
mode {‘full’, ‘same’, ‘valid’}の中から１つ (省略可能)初期値’full’
足し合わせを行う範囲を指定します。

returns:

aとvの畳み込み積分(畳み込み積分)を行った配列を返します。

ここでの畳み込み積分は、離散的な値にそって行われているので、以下のように表されます。

(a*v)[n] = \sum_{m=-\infty}^{\infty} a[m]v[n-m]

公式サイトの解説より

これは畳み込みニューラルネットワークで行っている畳み込み(convolution)と同じことを１次元で行っているとも言えます。畳み込みニューラルネットワークについては以下の記事を参考にしてください。

定番のConvolutional Neural Networkをゼロから理解する /deep_learning/2016/11/07/convolutional_neural_network.html

パラメータmodeについて

ここでのnの範囲を定めるのが引数modeとなります。モードごとの処理内容は以下の通りです。

  • full ： vの範囲いっぱいまでaの範囲内で積分を行うため、返される配列の長さはN+M-1となります。このとき、信号の残響を見ることができます。
  • same：配列の長さがmax(M,N)となり、長い方の配列に要素数を合わせます。
  • valid：うまくaとvの範囲が重ならない部分については結果を出力しません。そのため、配列の長さはabs(a-v)+1となります。

また、計算を行うときは、長い方の配列の要素１つ１つに対して短い方の配列の要素全てを掛け合わせたものを足し合わせるという操作を行っています。

図で解説

具体的な処理内容を分かりやすく図で解説してみます。np.convolve関数の引数aとvを以下のようなndarrayを指定することを考えてみます。

a = np.array([0, 1, 2, 3, 4, 5])
v = np.array([0.2, 0.8])

このパラメータを使用したときに、np.convolve関数のmodeによる違いを図示してみます。まず気をつけてほしいのは、vの要素の順番が処理を行う時に反対になっていることです。[0.2, 0.8]の順番になっていますが、処理の際は[0.8, 0.2]の順番となり反対になっています。

では、mode='full',mode = 'same'のとき前半の処理の仕方は同じで、以下の図のようになります。

解説1

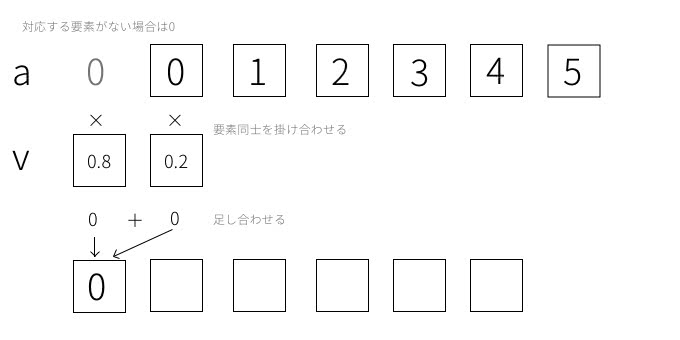
この操作を要素ごとに進めていきます。

解説2 解説3

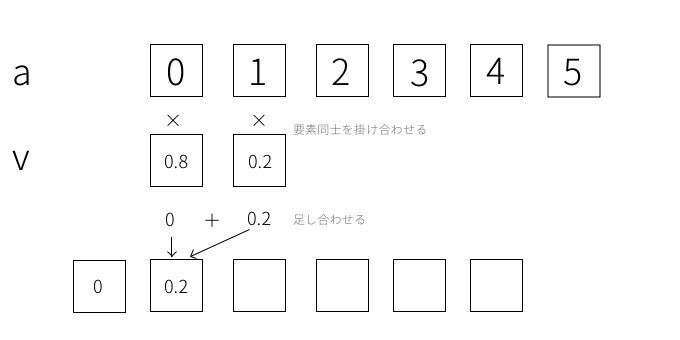
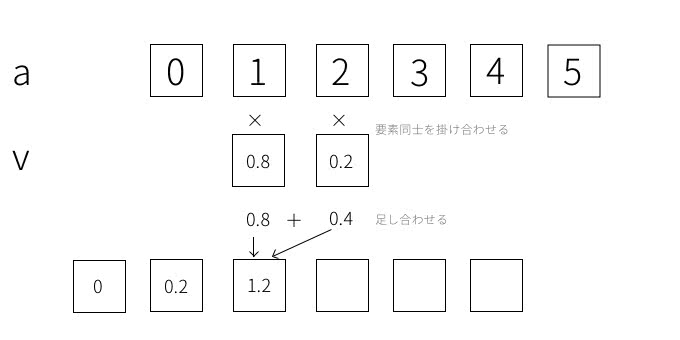
これが最後まできたときに’full’と’same’とで挙動が異なります。まずはmode='same'のときから説明します。このときはvがaの要素数からはみ出さない状態が最後の計算となり、以下の状態になったら処理が終了します。

same最後

一方、 mode='full'のときはvが最後まで行ききったら処理が終了します。今回の場合だと１つ分だけはみ出すことになります。

モードfull

次に、mode='valid'の場合について説明します。これは最初のスタートの位置が違っています。

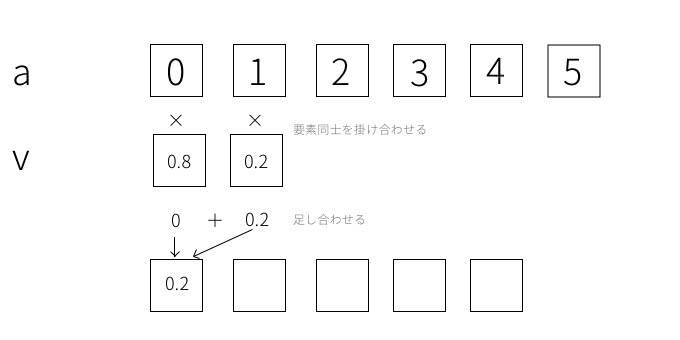
終点はmode='same'のときと同じです。

実際のコードで、結果が同じになっているか確かめましょう。

In [1]: import numpy as np

In [2]: a = np.array([0, 1, 2, 3, 4, 5]) # 配列a

In [3]: v = np.array([0.2, 0.8]) # 配列v

In [4]: np.convolve(a,v, mode='same') # まずは'same'から
Out[4]: array([ 0. ,  0.2,  1.2,  2.2,  3.2,  4.2])

In [5]: np.convolve(a, v, mode='full') # これがデフォルトの状態
Out[5]: array([ 0. ,  0.2,  1.2,  2.2,  3.2,  4.2,  4. ])

In [6]: np.convolve(a, v, mode='valid')
Out[6]: array([ 0.2,  1.2,  2.2,  3.2,  4.2])

図示した結果と一致していますね。

次に、移動平均を使ってノイズの混じったデータを平滑化してみましょう。サイン波を使って見ます。

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, 10, 500)
y1 = np.sin(x) # まずは元の信号を
y2 = y1 + np.random.randn(500)*0.3 # ノイズを混ぜる

v = np.ones(5)/5.0 # 移動平均をとるための配列vを設定。今回は前後５つの値を用いて平均をとる。
y3 = np.convolve(y2, v, mode='same')  # グラフを描く都合上'same'で。

plt.plot(x, y1,'r',linewidth=3)
plt.plot(x, y2,'b', linewidth=1)
plt.plot(x, y3, 'y',linewidth=1)
plt.show()

これで表示されたグラフは以下のようになります。赤い線が元のサイン波で、青い線がノイズ入りの信号、黄色い線が移動平均をとったものになります。

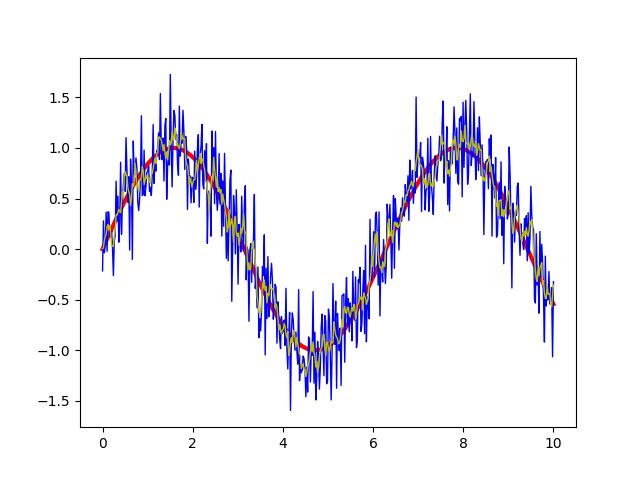
ある程度はノイズが軽減されていることがわかりますね。

畳み込み積分(畳み込み積分)

畳み込み積分(コンボリューション積分)は、主に電気回路の制御においてよく使われる手法で、入力信号に対して出力信号がどのようになるのかといったものを計算するためのものです。

畳み込み積分は、２つの関数を用いて表されます。定義として、f(t)とg(t) \\\\ の畳み込み積分f*g(\tau) \\\\ は以下のように表されます。

f*g(\tau) = \int f(t)g(\tau - t) dt

この積分の操作を畳み込み積分と呼びます。解析的にはこのように定義されるわけですが、実際のコードの中では離散値の和のかたちに直した形式として理解した方が使い勝手は良さそうです。

f*g(x) = \sum_{n} f(n)g(m-n)

wikipediaより

とはいえ、この２つの間に本質的な違いはありません。この式をどのような場面で使うかというと、f(t) を入力関数(時刻t にf(t) だけの入力があった)とし、g(t) を入力された信号が回路の中でどのように減衰していくかを表す関数だとします(この文章の中ではt=0 を最大値として単調減少していく関数を想定して話を進めます。また信号が入力される前は出力の仕様がないのでt<0 のときはg(t)=0 とします)。

このとき時刻\tau \\\\ の時点で、出力信号がどのようになっているのかを計算することになります。かなり前の時刻に入力された信号はほとんど無くなって、出力信号にはほとんど反映されないでしょうが、直近に入力された信号はまだ大きいままです。これらの信号の足し合わせが出力信号として出力されます。

この足し合わせを行うのが畳み込み積分となります。

また、音声や信号解析に使われるフーリエ変換でもよく用いられます。詳しい解説は、以下のサイトでわかりやすくされているので、詳しく知りたい方は参考にしてみてください。

参考