相関係数
相関係数とは、2組のデータの間にどれほどの関係性があるのかを示す1つの指標としてよく使用されます。
直線的な(線形的な)関係性を調べるための指標ですので、他の相関関係があったとしてもこの指標には現れにくいでしょう。値としては相関係数
の間で値をとります。ここで の絶対値が大きくなればなるほどその2つのデータの組の間には強い相関があるといえます。 ただし、相関係数の絶対値が大きいからといってその2つのデータの組の間に因果関係が成り立っているとは限らないので注意が必要です。もしかしたら他の要因が作用しているかもしれません。 また逆に0に近い値であっても、因果関係がないとは限らず、線形以外の相関関係がある可能性もあります。
定義
相関係数は2つのデータの組 と があるとし、 それぞれの分散を 、標準偏差を 、共分散を とすると、相関係数 は
となります。分母に分散の積の平方根をおき、分子に共分散の積をおくと相関係数を求めることができます。
| rの範囲 | 相関の度合い |
|---|---|
| -1 ≤ r < -0.7 | 強い負の相関 |
| -0.7 ≤ r < -0.4 | 負の相関 |
| -0.4 ≤ r < -0.2 | 弱い負の相関 |
| -0.2 ≤ r < 0.2 | 相関がほとんどない |
| 0.2 ≤ r < 0.4 | 弱い正の相関 |
| 0.4 ≤ r < 0.7 | 正の相関 |
| 0.7 ≤ r ≤ 1 | 強い正の相関 |
r の値によって相関関係は以上のような解釈をされることがあります。
r の値によって散布図がどのように変わるか見ていきましょう。以下のコードのcovの対角以外の成分を変更すると検証したいrの値になります。
In [1]: import numpy as np
In [2]: import matplotlib.pyplot as plt
In [3]: mean = np.array([0, 0]) # 平均を指定。
In [5]: cov = np.array([
...: [1, 0.8],
...: [0.8, 1]]) # 共分散行列を指定。2つの0.8のところを好きなrの値に変えればxとyの共分散の値を変えられる。
In [6]: x, y = np.random.multivariate_normal(mean, cov, 5000).T # とりあえず5000個生成。
In [7]: plt.plot(x, y, 'x') # プロットする。
Out[7]: [<matplotlib.lines.Line2D at 0x1139f0d68>]
In [8]: plt.title("r=0.8")
In [9]: plt.axis("equal")
Out[9]:
(-3.7646535119201965,
3.6544589032268662,
-3.8254227272245971,
4.1194358830470321)
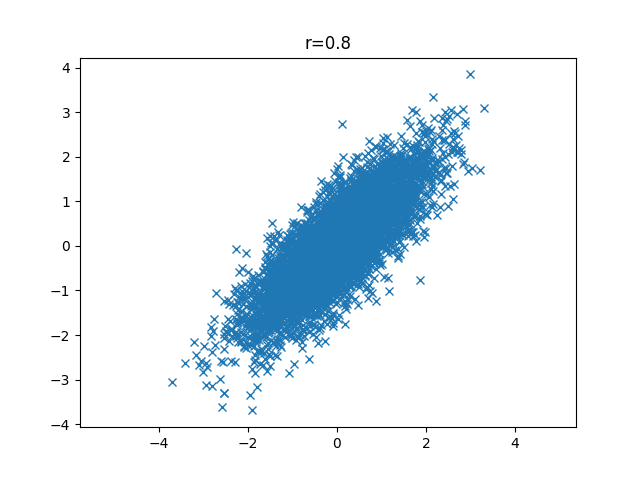
In [10]: plt.show()このコマンドを実行することで得られるグラフは以下のようになります。まずはr=0.8の場合から確認してみます。このグラフから強い正の相関があることがわかります。
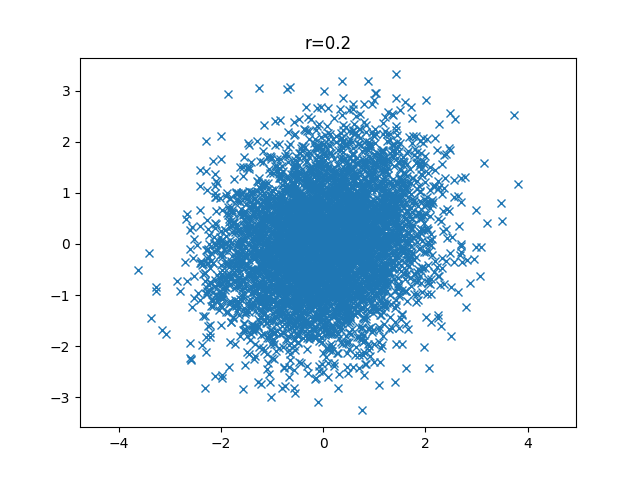
次はr=0.2相関関係がわかりにくくなってますね。
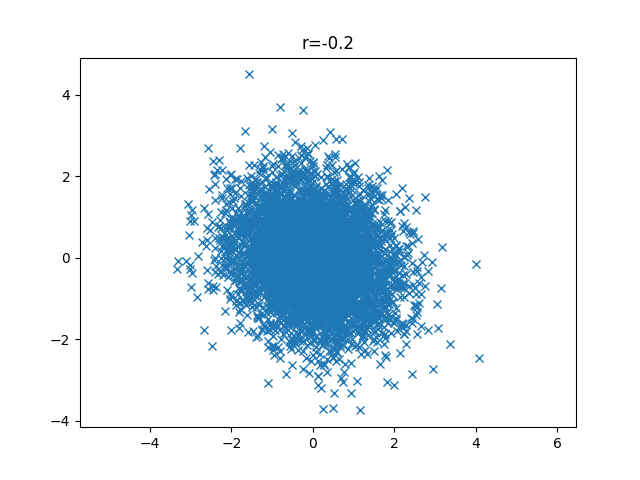
次はr=-0.2です。負の値なので若干右肩下がりになっています。
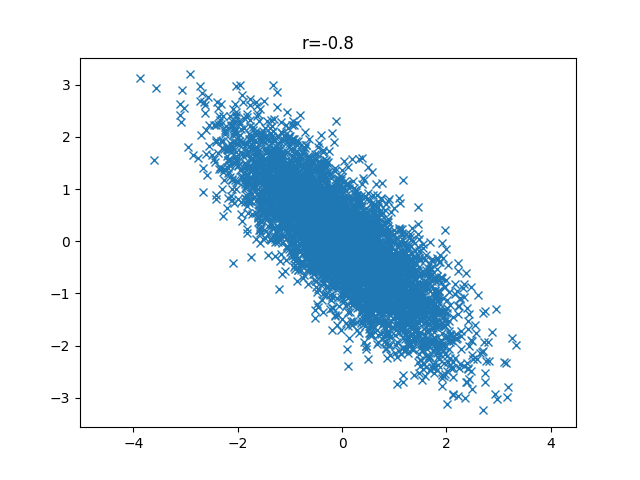
最後にr=-0.8です。右肩下がりが顕著に出ているのがわかりますね。
np.corrcoef関数
相関係数について簡単におさらいしたところで次は関数自体の使い方について扱っていきます。
相関係数って英語で”correlation coefficients”というのでそれを縮めてcorrcoefになっているみたいです。読み方が分からないですね…。
APIドキュメント
np.corrcoef関数のAPIドキュメントは以下のとおりです。
**np.corrcoef(x, y=None, rowvar=True, bias=_NoValue, ddof =
params:
| パラメータ名 | 型 | 概要 |
|---|---|---|
x |
配列に相当するもの | 複数回の観測値が含まれている1次元か2次元の配列を指定します。 |
y |
配列に相当するもの | (省略可能)初期値None 追加するデータを指定します。xとyがそれぞれ1次元配列で結合する手間なくその2つの相関係数を知りたいときなどによく使います。 |
rowvar |
bool値 | (省略可能)初期値True 行ごとの相関係数を知りたいときはここをTrueにします。そうではなく、列ごとの相関係数を知りたいときはここをFalseにします。 |
bias |
no value | ここ使わないほうがよいそうです。 |
ddof |
no value | ここも上と同様使わないようがよいそうです。 |
dtype |
データ型 | (省略可能)初期値None。結果のデータ型。デフォルトでは、返されるデータ型は少なくともnumpy.float64の精度をもつ |
returns:
相関係数を要素に持つ行列が返されます。
ddofとbiasは引数として何か指定しても意味がないそうなので、ここは気にしなくて大丈夫です。
最低限指定すべきなのは相関係数を求めたいデータのセットを入力するxで、結合するのが面倒なときにはyを使います。
また、データセットが列ごとに別れていたら、rowbar=Falseにして対応します。
相関係数を求める
では、実際に使いながら確認してみます。まずは適当に値を生成して、その値を見比べてみます。
今回は1行目に数学のテストの点数(10点満点)、2行目に国語のテストの点数(10点満点)を生徒ごとに記載していくことにします。
国語の成績と数学の成績の相関関係をみていくという目的でnp.corrcoef関数を使っていきます。
In [1]: import numpy as np
In [2]: x = np.array([
...: [1, 2, 1, 9, 10, 3, 2, 6, 7],
...: [2, 1, 8, 3, 7, 5, 10, 7, 2]]) # 1行目が数学、2行目が国語の成績。
...:
In [3]: np.corrcoef(x) # 相関関数行列を求める。
Out[3]:
array([[ 1. , -0.05640533],
[-0.05640533, 1. ]])
In [4]: # 右上と左下の値が相関係数となっている。2つの配列から相関係数を求める
この値を見てみると、ほぼ0となっているので国語と数学の成績にはほとんど相関関係がないということがわかります。では、ここに英語の成績を 追加してみましょう。
In [5]: y = np.array([2, 1, 1, 8, 9, 4, 3, 5, 7]) # 英語の成績を追加。
In [6]: np.corrcoef(x, y) # 第二引数としてyを入れることで3つの科目の成績をわざわざ結合しなくても相関係数を求めることが可能になる。
Out[6]:
array([[ 1. , -0.05640533, 0.97094584],
[-0.05640533, 1. , -0.01315587],
[ 0.97094584, -0.01315587, 1. ]])最後に得られた3次元行列を見ていきます。これは以下の表のように2つの科目の相関係数となります。
| 数学 | 国語 | 英語 | |
|---|---|---|---|
| 数学 | 数学-数学 | 数学-国語 | 数学-英語 |
| 国語 | 国語-数学 | 国語-国語 | 国語-英語 |
| 英語 | 英語-数学 | 英語-国語 | 英語-英語 |
科目が同じところは同じ科目同士で比べているので相関係数は1となります。
これを踏まえて上の行列を見てみると、数学と英語の相関係数が0.97ととても1に近い値になっており、強い相関を持っていることがわかります。しかし、数学と国語、英語と国語についてはどちらも0に近い値となっており、相関関係は認められません。
このことから、数学と英語の成績には正の相関が認められるが、他のものについては相関関係は認められなかったというのがこの相関係数行列の意味するところです。
では次にデータの縦と横を入れ替えたときに活躍するrowvarを使ってみます。
ここで求めているのはある生徒と生徒同士の点数の相関係数で、例えばその生徒が良い点数を取った時に、もう一人の生徒はそれにつられて良い点数をとる傾向があるのかどうかを求めているということになります。
In [7]: x_transpose = x.T
In [8]: np.corrcoef(x_transpose, rowvar=False) # rowvar=Falseにすることで列ごとに相関係数を求める。
Out[8]:
array([[ 1. , -0.05640533],
[-0.05640533, 1. ]])
In [11]: np.corrcoef(x_transpose, rowvar=True) # rowvar=True(デフォルト)のままにすると生徒ごとの相関係数を求めることになる。
Out[11]:
array([[ 1., -1., 1., -1., -1., 1., 1., 1., -1.],
[-1., 1., -1., 1., 1., -1., -1., -1., 1.],
[ 1., -1., 1., -1., -1., 1., 1., 1., -1.],
[-1., 1., -1., 1., 1., -1., -1., -1., 1.],
[-1., 1., -1., 1., 1., -1., -1., -1., 1.],
[ 1., -1., 1., -1., -1., 1., 1., 1., -1.],
[ 1., -1., 1., -1., -1., 1., 1., 1., -1.],
[ 1., -1., 1., -1., -1., 1., 1., 1., -1.],
[-1., 1., -1., 1., 1., -1., -1., -1., 1.]]) 人工知能の今と一歩先を発信するメディア
人工知能の今と一歩先を発信するメディア