今回は、共分散(covariance)を求めてくれる関数np.cov()について扱っていきたいと思います。
まずは共分散の簡単な復習からしましょう。
共分散
共分散というのは、二組の対応するデータがどれほどお互いに影響を持ちながら散らばっているかを表します。
この値がそれぞれのデータの持つ分散に近いほどこの二組のデータの相関性は強くなります。(これを相関係数と呼びます。)
共分散が負であれば負の相関(一方の値が増えるともう一方の値が減少する)があり、正であれば正の相関があるといえます。
まずは定義式を見てみます。
あるデータの組とがあるとします。
この2つのデータの組の共分散をとすると、
ここで、はそれぞれの要素の平均となっています。
式の中身を見てみると、これはの各々の要素から平均を差し引いたものの掛け算を足し合わせています。
そして最後にこれを値の個数であるで割ることにより共分散を求めています。
このとき、とが一致していれば、それはの分散を求めていることになります。
ちなみに、ここのをにすると不偏共分散と言われる、ある母集団からサンプリングした場合のサンプリングされた値から推測される共分散を示します。
また各々の相関を調べたいデータの組が2つ以上存在するとき共分散行列というものがよく使われます。
これは対角成分が各々のデータの分散を示しており、そのほかの成分がある組とある組との共分散を示しています。
例えば、の共分散行列は以下のようになります。
ここで、はの共分散を示しており、ただのかける順序を入れ替えただけなので値は一緒になります。
また、で分散を表しています。
データの組でを追加した共分散行列を見てみます。
これは以下のようになります。
では、1つ例として共分散を指定した2つのデータの組を生成して、グラフにプロットしてみます。
2つのデータの平均と分散をそれぞれ0と1に固定して、共分散の値だけ変えていきます。
ここに出てくるnp.random.multivariate_normal()関数は指定された平均と共分散行列に沿ったランダムな値を生成してくれる関数です。
In [1]: import numpy as np
In [2]: import matplotlib.pyplot as plt
In [3]: mean = np.array([0, 0]) # 平均を指定。
In [5]: cov = np.array([
...: [1, 0.1],
...: [0.1, 1]]) # 共分散行列を指定。0.1のところを変えればxとyの共分散の値を変えられる。
In [6]: x, y = np.random.multivariate_normal(mean, cov, 5000).T # とりあえず5000個生成。
In [7]: plt.plot(x, y, 'x') # プロットする。
Out[7]: [<matplotlib.lines.Line2D at 0x1139f0d68>]
In [8]: plt.title("covariance = 0.1")
In [9]: plt.axis("equal")
Out[9]:
(-3.7646535119201965,
3.6544589032268662,
-3.8254227272245971,
4.1194358830470321)
In [10]: plt.show()covの右上と左下の値が共分散に相当するのでここを0.1~1の範囲で変えてみます。
まずは0.1の場合から。
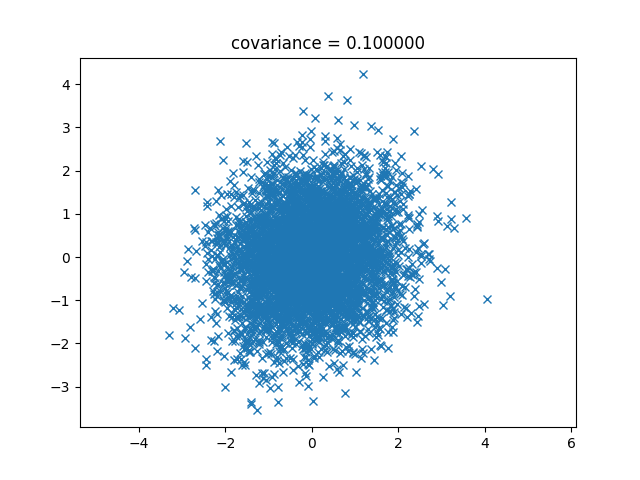
次は0.3。
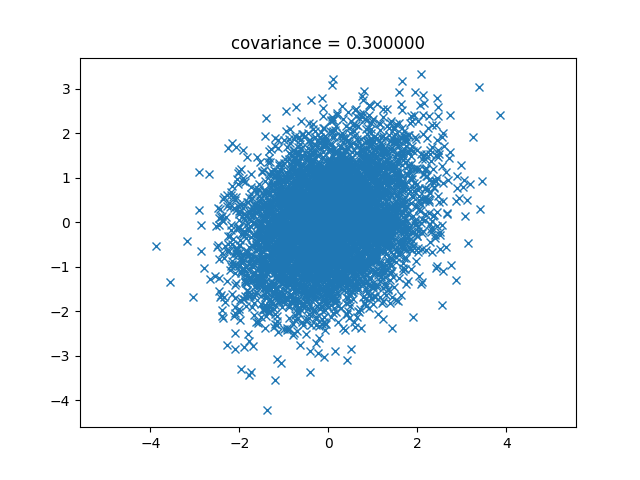
次は0.5です。
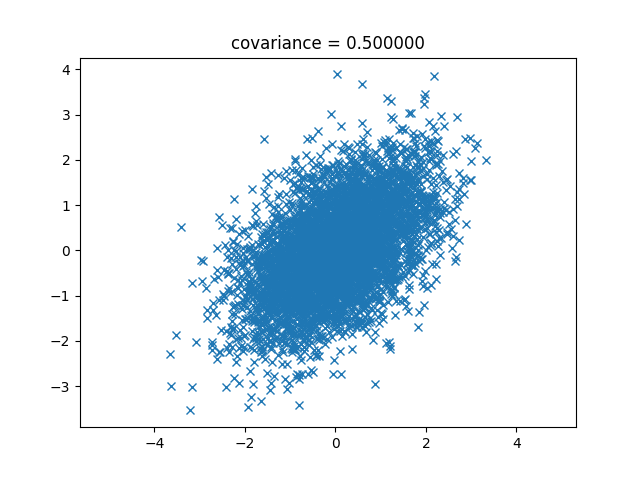
次は0.7です。
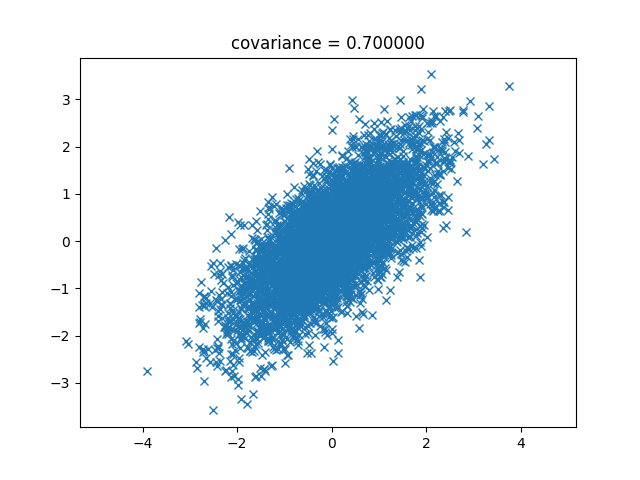
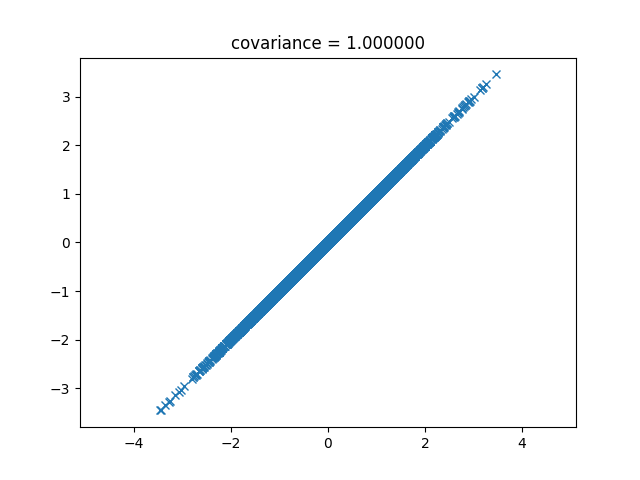
次は1です。これは直線になります。
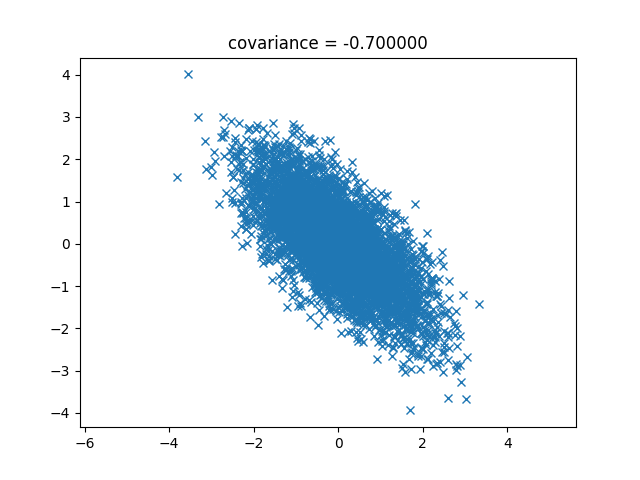
最後に負の値である-0.7をみてみます。これは負の相関になっていることがわかりますね。
np.cov()
それでは、関数の使い方について見ていきましょう。
APIドキュメント
np.cov()関数のAPIドキュメントは以下のとおりです。
np.cov(m, y=None, rowvar=True, bias=False, ddof=None, fweights=None, aweights=None, …, dtype=None)
params:
| パラメータ名 | 型 | 概要 |
|---|---|---|
m |
配列に相当するもの | 1次元か2次元配列。それぞれの行にはデータの組が入っており、行の数がデータの組の個数を示します。同じ列のデータが1回の観測で得られたデータと捉えます。 |
y |
配列に相当するもの | (省略可能)初期値None mに付け加える値を指定します。mに含まれるデータの組と同じ形状(shape)である必要があります。 |
rowvar |
bool値 (TrueかFalse) |
(省略可能)初期値True ここがTrueだと各々の行が1つのデータの組だとみなされます。共分散を求める際は行間で求めます。Falseの場合、各々の列が1つのデータの組となります。 |
bias |
bool値 (TrueかFalse) |
(省略可能)初期値False ここがFalseだと不偏共分散を求めることになります。つまり、平均との偏差の積の和を(データ数 - 1)で割ることになります。Trueにすると(データ数)で割ります。 |
ddof |
int | (省略可能)初期値None ここがNoneでないと、biasによって設定された値が上書きされます。ddof=1のときは標準共分散(足し合わせた積の値をデータ数nで割る)となります。ddof=0のときは平均を返します。 |
fweights |
配列に相当するもの またはint |
(省略可能)初期値None 1観測(列ごとの値)ごとにつける重みを設定します。 |
aweights |
配列に相当するもの | (省略可能)初期値None それぞれのデータの組ごと(行ごとの値)にかけられる重みを指定します。観測で重要な値についてはここの重みを大きくし、重要性が低いものについては重みを小さくします。ddof=0の場合、ここで指定される値は無視されます。 |
dtype |
データ型 | 結果のデータ型を指定する。デフォルトではnumpy.float64以上の精度になる。 |
returns:
指定されたデータ組による共分散行列が返されます。
かなり引数が多くて大変ですね。頻繁に使う引数はm以外には値を追加できるyになります。
このyの使い方がわかるとわざわざデータを1つの配列に統合してから値を求める必要がなくなるので、便利です。
他の引数としては、データの組を行ごとに1つの種類と見るのではなく、列を1つの種類のデータとみなすかどうかを選択するrowvarや、標本分散か不偏分散を求めるかを指定できるbiasがあります。他にも、共分散の求め方を指定するddofや、列(1回分の観測データ)ごとの繰り返しを指定できるfweightsや、列ごとに重みをつけられるaweightsがあります。
サンプルコード
APIドキュメントをみたところで、次は実際に使っていきましょう。
まずは、m単体とyを追加するところをやってみましょう。
In [1]: import numpy as np
In [2]: a = np.array([[10, 5, 2, 4, 9, 3, 2],[10, 2, 8, 3, 7, 4, 1]])
In [3]: # 1行目を各生徒の数学の点数、2行目を各生徒の国語の点数(それぞれ10点満点)としている。
In [4]: np.cov(a) # まずは引数mにaだけを指定する。
Out[4]:
array([[ 10.66666667, 6.66666667],
[ 6.66666667, 11.33333333]])
In [5]: c = np.array([3, 2, 1, 5, 7, 2, 1]) # 今度は英語の点数を追加する。
In [6]: np.cov(a,c) # 引数yにcを指定する。数学、国語、英語の共分散行列が返される。
Out[6]:
array([[ 10.66666667, 6.66666667, 4.66666667],
[ 6.66666667, 11.33333333, 1.66666667],
[ 4.66666667, 1.66666667, 5. ]])次にrowvar = False(初期値はTrue)にして、各列が教科の点数に対応しているとします。
In [7]: a_transpose = a.T # 列と行を入れ替える。
In [11]: c_transpose = np.reshape(c, (-1, 1))
In [12]: np.cov(a_transpose, y=c_transpose, rowvar=False)
Out[12]:
array([[ 10.66666667, 6.66666667, 4.66666667],
[ 6.66666667, 11.33333333, 1.66666667],
[ 4.66666667, 1.66666667, 5. ]])次は標本分散(得られたデータを母集団そのものとして見て得る共分散や分散)を求めてみます。
bias = True(初期値False)にすることでできます。
In [18]: np.cov(a, bias=False) # まずは初期値の方から。
Out[18]:
array([[ 10.66666667, 6.66666667],
[ 6.66666667, 11.33333333]])
In [19]: np.cov(a, bias=True) # Nで割るので値が少しずつ減少する。
Out[19]:
array([[ 9.14285714, 5.71428571],
[ 5.71428571, 9.71428571]])次にddofの値を変更してみます。ddofの値を増やすことで偏差の積を割る値を減らすことになります。
不偏分散を求める場合はddof=1、標本分散を求める場合はddof=0にして全体のサンプル数から引く値を指定しています。
In [23]: np.cov(a, ddof=None)
Out[23]:
array([[ 10.66666667, 6.66666667],
[ 6.66666667, 11.33333333]])
In [24]: np.cov(a, ddof=0)
Out[24]:
array([[ 9.14285714, 5.71428571],
[ 5.71428571, 9.71428571]])
In [25]: np.cov(a, ddof=1)
Out[25]:
array([[ 10.66666667, 6.66666667],
[ 6.66666667, 11.33333333]])
In [26]: np.cov(a, ddof=2)
Out[26]:
array([[ 12.8, 8. ],
[ 8. , 13.6]])次に同じ点数の生徒が2人いた場合などに使うfweightsを指定します。
ここで指定された回数分だけ重複してそのデータはカウントされます。
In [27]: a
Out[27]:
array([[10, 5, 2, 4, 9, 3, 2],
[10, 2, 8, 3, 7, 4, 1]])
In [28]: # 左から2,3番めの生徒の点数を重要視する。
In [29]: fweights = np.array([1, 2, 2, 1, 1, 1, 1])
In [30]: np.cov(a, fweights=fweights)
Out[30]:
array([[ 9. , 3.875],
[ 3.875, 10.75 ]])最後に観測(生徒)ごとに重みをつけるaweightsです。
これは先程とは違い、ある列(生徒)の値を大きくすると他の列(生徒)の値の重要性が相対的に減少します。
fweightsとは異なり回数ではなく重みを設定します。
In [42]: aweights= np.array([0.1, 0.2, 0.2, 0.2, 0.1, 0.1, 0.1]) # 2,3,4番目の生徒の点数を重視する。
In [43]: np.cov(a, aweights=None)
Out[43]:
array([[ 10.66666667, 6.66666667],
[ 6.66666667, 11.33333333]])
In [44]: np.cov(a, aweights=aweights)
Out[44]:
array([[ 8.61904762, 3.83333333],
[ 3.83333333, 10.66666667]])参考
・numpy.random.multivariate_normal — NumPy v1.13 Manual
・共分散の意味と求め方、共分散公式の使い方 - Sci-pursuit
・numpy.cov — NumPy v1.13 Manual - Numpy and Scipy Documentation
 人工知能の今と一歩先を発信するメディア
人工知能の今と一歩先を発信するメディア