rolling関数は窓関数と呼ばれるものを指定した要素の数の幅だけ適用する関数となっており、窓関数を適用することでそれぞれの要素に重みがついたものがそれぞれの要素に格納されています。
rolling関数は移動平均を求める際に利用されたりするもので、時系列データ分析ではよく使用されるので覚えておくと便利です。
窓関数の詳しい解説は後述します。
まずはrolling関数そのものの使い方を見ていきましょう。
rolling関数
rolling関数が行う処理はNumPyのconvolve関数に似ている部分があります。
convolve関数は指定した重みで足し合わせていく操作も一度も行っており、rolling関数は要素に重みをつけるだけであり、それを使って何かしらの計算をする関数を付け加える必要があります。
対象とする要素の数を指定する(窓の幅を指定する)
第一引数であるwindowを指定することで、重みを付け加えていく要素の数を指定します。
例えばwindow=2の場合、対象とする要素と1つ後ろの要素までを計算の対象に入れることになります。
デフォルトではそれぞれの要素の重みは一律で1 となっています。
計算結果は対象とする要素の和にします。
In [1]: import pandas as pd
In [2]: sr = pd.Series(range(10))
In [3]: sr
Out[3]:
0 0
1 1
2 2
3 3
4 4
5 5
6 6
7 7
8 8
9 9
dtype: int64
In [4]: sr.rolling(3) # 対象とする要素数は3。これだけだと結果は返ってこない
Out[4]: Rolling [window=3,center=False,axis=0]
In [5]: sr.rolling(3).sum() # 自身も含めた後ろ3つの要素の和を取る
Out[5]:
0 NaN
1 NaN
2 3.0
3 6.0
4 9.0
5 12.0
6 15.0
7 18.0
8 21.0
9 24.0
dtype: float64
デフォルトでは対象となる要素がwindowで指定した個数に満たない場合はNaN値となります。
例えば、2番目の要素の結果は3.0となっていますが、これは新しい2番目の要素をと表現するとすると、
の結果となっており、自信を含めて後ろ3つの値の和を求めています。(meanを指定すれば平均を求めてくれます。)
また1.0をかけていますが、これがいわゆる重みです。デフォルトでは一律で1がかかっており、これらの値を変更する際はwin_typeで重みの種類を変更します。
対象とする要素の最小個数を設定
min_periodsを指定することで、先ほどはwindowで指定した値の個数よりも少ない場合はNaN値となっていたものを減らすことができます。
min_periods=1とすれば全ての要素が対象となります。
In [7]: sr.rolling(3, min_periods=1).sum() # NaN値がなくなる
Out[7]:
0 0.0
1 1.0
2 3.0
3 6.0
4 9.0
5 12.0
6 15.0
7 18.0
8 21.0
9 24.0
dtype: float64
基準点の前後を対象とする
先ほどは、window=3の場合、以下のような式で値を求めることができました。
この式では、対象インデックスよりも前のインデックス分に窓を適用します。
対象インデックスを中心として窓関数を適用したい場合もありそうです。対象となっている要素を中心に前後の足し合わせをつくると以下のようになります。
一般化をすると以下のような書き方になります。i番目の要素について
このような計算をしたい場合はcenter=Trueにします。
In [9]: sr.rolling(3,center=True).sum()
Out[9]:
0 NaN
1 3.0
2 6.0
3 9.0
4 12.0
5 15.0
6 18.0
7 21.0
8 24.0
9 NaN
dtype: float64
In [10]: sr.rolling(3).sum() # 元の結果と比べると1つずつ値がシフトしているのがわかる
Out[10]:
0 NaN
1 NaN
2 3.0
3 6.0
4 9.0
5 12.0
6 15.0
7 18.0
8 21.0
9 24.0
dtype: float64
時系列の間隔を指定
時系列データに対しては時間の間隔を指定することができます。 以下のようなインデックスが時刻となっているものを作成します。
In [11]: index = pd.date_range('1/1/2018',periods=20)
In [12]: sr_time = pd.Series(range(20), index=index)
In [13]: sr_time
Out[13]:
2018-01-01 0
2018-01-02 1
2018-01-03 2
2018-01-04 3
2018-01-05 4
2018-01-06 5
2018-01-07 6
2018-01-08 7
2018-01-09 8
2018-01-10 9
2018-01-11 10
2018-01-12 11
2018-01-13 12
2018-01-14 13
2018-01-15 14
2018-01-16 15
2018-01-17 16
2018-01-18 17
2018-01-19 18
2018-01-20 19
Freq: D, dtype: int64
ではこれを3日の幅でサンプリングして見ましょう。
In [14]: sr_time.rolling('3D').sum()
Out[14]:
2018-01-01 0.0
2018-01-02 1.0
2018-01-03 3.0
2018-01-04 6.0
2018-01-05 9.0
2018-01-06 12.0
2018-01-07 15.0
2018-01-08 18.0
2018-01-09 21.0
2018-01-10 24.0
2018-01-11 27.0
2018-01-12 30.0
2018-01-13 33.0
2018-01-14 36.0
2018-01-15 39.0
2018-01-16 42.0
2018-01-17 45.0
2018-01-18 48.0
2018-01-19 51.0
2018-01-20 54.0
Freq: D, dtype: float64
この場合、時間の間隔ごとにまとめて 処理をしているので必要最低限のデータ数という縛りが無くなります。そのため、データ数が足りないことが原因によるNaN値が無くなります。
7日ごとであるなら'7D'と指定します。
In [20]: sr_time.rolling('7D').sum()
Out[20]:
2018-01-01 0.0
2018-01-02 1.0
2018-01-03 3.0
2018-01-04 6.0
2018-01-05 10.0
2018-01-06 15.0
2018-01-07 21.0
2018-01-08 28.0
2018-01-09 35.0
2018-01-10 42.0
2018-01-11 49.0
2018-01-12 56.0
2018-01-13 63.0
2018-01-14 70.0
2018-01-15 77.0
2018-01-16 84.0
2018-01-17 91.0
2018-01-18 98.0
2018-01-19 105.0
2018-01-20 112.0
Freq: D, dtype: float64
窓関数を変更する
win_type引数で窓関数の種類を変更することが可能です。
詳しくはページの後半で解説するのでそちらを参照してください。
窓関数に三角波triangを適用して見ます。
In [22]: sr.rolling(5,win_type='triang').sum()
Out[22]:
0 NaN
1 NaN
2 NaN
3 NaN
4 6.0
5 9.0
6 12.0
7 15.0
8 18.0
9 21.0
dtype: float64
In [23]: sr.rolling(5).sum() # 値が異なっているのがわかる
Out[23]:
0 NaN
1 NaN
2 NaN
3 NaN
4 10.0
5 15.0
6 20.0
7 25.0
8 30.0
9 35.0
dtype: float64
移動平均を求める
rolling関数にmeanを使えば簡単に移動平均を求めることができます。
例えば、ランダムウォークの問題などで考えて見ましょう。
NumPyの関数を使ってランダムウォークの値を作ります。
In [55]: import numpy as np
In [56]: random_walk = np.random.choice([-1,1],size=1000) # 1か-1の値を1000個生成
In [57]: random_walk = random_walk.cumsum() # 1つずつ足し合わせて行った値を要素にいれていく
In [58]: random_sr = pd.Series(random_walk)
In [59]: import matplotlib.pyplot as plt # matplotlibを使ってグラフの描画
In [60]: random_sr.plot()
Out[60]: <matplotlib.axes._subplots.AxesSubplot at 0x101612da0>
In [61]: plt.xlabel('time') # x軸のラベル設定
Out[61]: Text(0.5,0,'time')
In [62]: plt.ylabel('walk') # y軸のラベル設定
Out[62]: Text(0,0.5,'walk')
In [63]: plt.title('random_walk') # タイトル設定
Out[63]: Text(0.5,1,'random_walk')
In [64]: plt.grid() # グリッド表示
In [66]: plt.show()
これで表示されるグラフは以下のようになります。
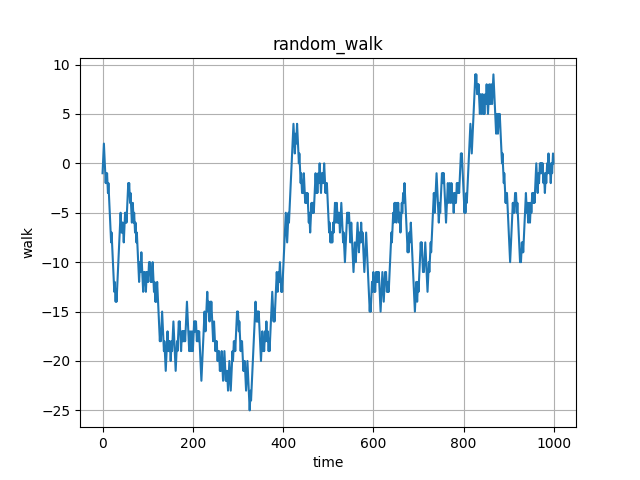 かなりガタついたグラフが表示されました。
この変化の様子をより滑らかに見たい時に移動平均と呼ばれる周囲いくつかの要素の値の平均を取る手法を使います。
かなりガタついたグラフが表示されました。
この変化の様子をより滑らかに見たい時に移動平均と呼ばれる周囲いくつかの要素の値の平均を取る手法を使います。
これの移動平均を求めていきます。
窓の幅を10くらいにして見ます。
In [67]: roll_mean = random_sr.rolling(10).mean() # 移動平均を求める
In [80]: random_sr.name = 'original' # グラフに表示できるよう名称を設定しておく
In [81]: roll_mean.name = 'rolled'
In [82]: random_sr.plot() # 比較用に移動平均を求める前のものをプロットする
Out[82]: <matplotlib.axes._subplots.AxesSubplot at 0x10d27cfd0>
In [83]: roll_mean.plot() # 移動平均を求めたものをプロット
Out[83]: <matplotlib.axes._subplots.AxesSubplot at 0x10d27cfd0>
In [84]: plt.legend() # 凡例
Out[84]: <matplotlib.legend.Legend at 0x10d264320>
In [85]: plt.xlabel('time')
Out[85]: Text(0.5,0,'time')
In [86]: plt.ylabel('walk')
Out[86]: Text(0,0.5,'walk')
In [87]: plt.grid()
In [88]: plt.title('random walk')
Out[88]: Text(0.5,1,'random walk')
In [89]: plt.savefig('random_walk_rolling.png')
In [90]: plt.show()
表示される結果は以下のようになります。
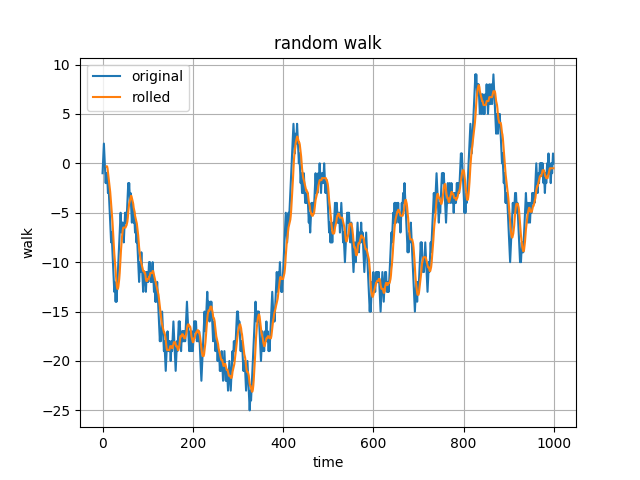
先ほどよりもグラフが滑らかになり、変化の様子が分かりやすくなりました。
窓関数について
rolling関数の引数の中でwin_typeがありました。これは適用する窓関数の種類を指定できるものとなっています。
ここでは窓関数について内容を知りたいと言う方のために簡単に解説します。
窓関数とは、使う意味
窓関数は信号を離散フーリエ変換する際のサンプリング間隔に関する問題を解決するためによく使われるもので、ただ単純に一定区間の信号を抜き出すより実際のデータに近い周波数を抜き出すことが可能となります。
以下のような信号があったとして、青い枠の範囲内でサンプリングをしたとします。フーリエ変換の際はこの区間が無限に続くものとして周波数領域への変換を行います。

すると、変換の際は以下のような波形を変換していることになり、元のものとはだいぶ違った形となっていることがわかると思います。

スペクトル解析と窓関数 より
このようなサンプリング間隔と周期の不一致は必ず起きる問題であり、避けられない問題です。そのため、この影響を小さくするために考案されたのが窓関数です。
どういうものかというと、データに対して、一定の分布にしたがってそれぞれの値に対して重みをつける関数となります。
ここで重要なのは重みをつけるだけの操作しかしないということで、あくまで何かしらの処理を行うための前段階に行うものとなります。 信号処理の場合は大抵、窓関数を適用したのち、フーリエ変換を施して周波数領域へと変換するという流れになります。
窓関数を使う目的がわかったところで、引数win_typeで指定できる窓関数の種類について一部を紹介します。
窓関数の種類(win_type)について
一番単純なものは全てのデータに対して一様な重みをつけるもので、グラフだと以下のような形状になります。
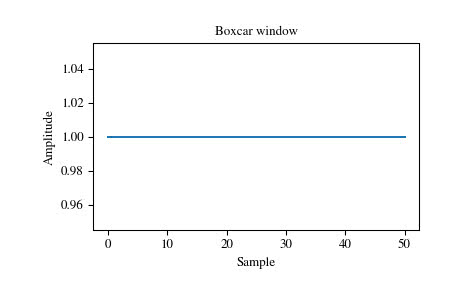
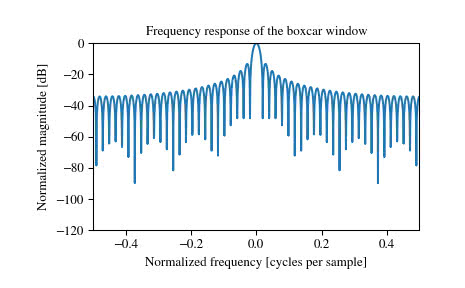
scipy.signal.windows.boxcar — SciPy v1.1.0 Reference Guide より
上側が、時系列に沿ったグラフの形状で、下側がそれをフーリエ変換した後の形状となっています。
これは与えられた信号がそのまま出力されることになります。
rolling関数のwin_typeで言うとNoneもしくはboxcarに相当するものです。単純な足し合わせをしたい時にはこれで十分でしょう。
次に三角波です。三角形をしています。win_type='triang'で指定することができます。
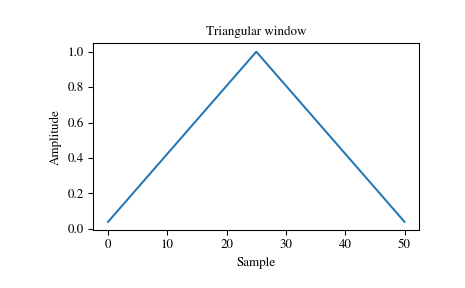
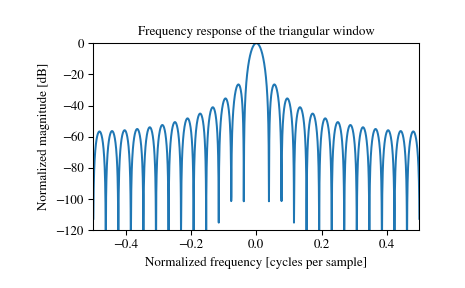
scipy.signal.windows.triang — SciPy v1.1.0 Reference Guide より
次にガウシアンです。領域の広がり具合だけ指定する必要があります。win_type='gaussian(0.1)'のように指定します。
以下の数式で定義されます。
ここで、 が標準偏差となっており、こちらで指定する必要のある値です。
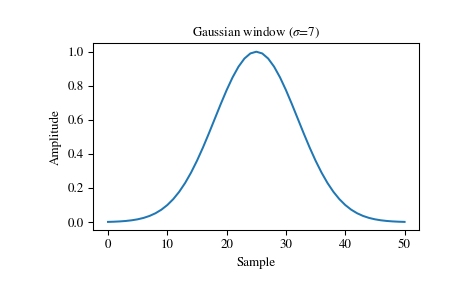
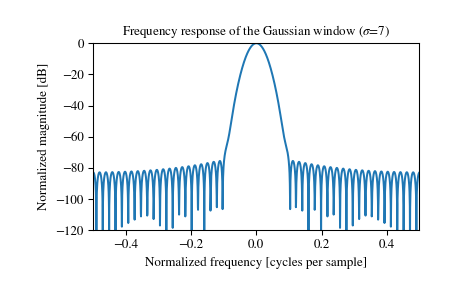
scipy.signal.windows.gaussian — SciPy v1.1.0 Reference Guide より
公式ドキュメントによるとこのほかにも様々な窓関数が実装されています。
以下、公式ドキュメントに掲載されていたwin_type一覧です。
boxcar
triang
blackman
hamming
bertlett
parzen
bohman
blackmanharris
nuttall
barthann
kaiser (betaを指定する必要あり)
gaussian (stdを指定する必要あり)
general_gaussian (power,widthを指定する必要あり)
slepian (widthを指定する必要あり)
実装自体はscipy.signal.windowsにある関数をそのまま使っているだけなので、どんな関数があるのかは以下のページを見ると参考になると思います。
Window functions (scipy.signal.windows) - SciPy v1.1.0 Reference Guide
もっと詳しく知りたい方は以下のサイトを参照してみてください。
 人工知能の今と一歩先を発信するメディア
人工知能の今と一歩先を発信するメディア