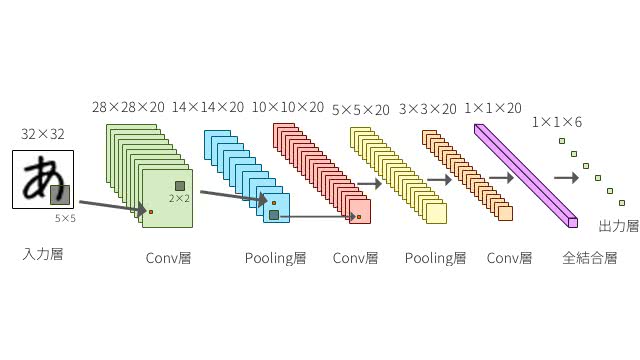
誤差逆伝播法（Backpropagation）は、ニューラルネットワークの基本アルゴリズムです。 本質的な仕組みを理解していると、ディープラーニングがどのように動作しているのかのイメージを掴むことができます。 つまり、誤差逆伝播法の仕組みを知ることは、ニューラルネットワークの開発やデバッグ・設計において重要な役割を果たすのです。

にも関わらず、解説を読むと、突然偏微分を含む数式が出てきたりするので、難解なイメージを持つ方が多いのではないでしょうか。

本記事は、誤差逆伝播法を計算グラフと具体的な例を示しながら、噛み砕いて解き明かそうとする試みになります。

おそらく、あなたが誤差逆伝播法を理解する手助けになるはずです。

誤差逆伝播法とパラメータ

誤差逆伝播法は、損失関数の微分を高速に計算する手法です。 ニューラルネットワークが正しい答えを導き出せるようにするためには、

(1) 正解の入力値と出力値を渡す
(2) 入力から得られた出力と正解の出力との誤差を計算する損失関数を設定する
(3) 損失が最小になるパラメータを発見する

というステップで得られたパラメータを使って、ネットワークを学習して欲しい関数に近似させます。 実際には、損失関数さえ設定できれば、(1)のステップはBackpropのためには必ずしも必要ではないのですが、イメージしやすいので記述しています。

ネットワークのパラメータ w_{i} をどのように変化させれば損失は小さくなるのでしょうか。

簡略化すると下図のように、損失関数のグラフ上でパラメータ w_{i} での傾きを計算すると、より小さくなる方向が分かるので、その方向に少量ずつ近づけることが考えられます。

傾きの図

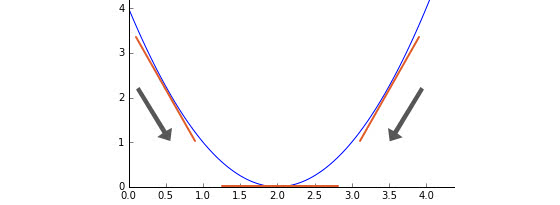
この図の場合、w_{i} が2に近づくほど出力は0に近づいていきます。もし w_{i} が1であれば、傾きは負の値になりますから、w_{i} を大きくすれば、損失関数の出力は小さくなります。 つまり、局所的な傾きをとることで、ネットワーク全体の出力が小さくなる方向にパラメータを調節することが可能になります。 損失関数のあるパラメータでの偏微分（局所的な微分）の大きさは、出力に対するパラメータの影響度合いを意味しています。

計算グラフ

計算グラフは、誤差逆伝播法を理解する上で重要な概念です。 グラフでの演算とデータの表現とシンボルを割り当てながら計算を遅らせて評価する遅延評価の特性が、誤差逆伝播法と非常に相性が良いからです。

計算グラフは、演算とデータをノードとエッジで表現する方法です。 例えば、(a \times b) + (c \times d) という数式を計算グラフで表現すると、以下の図のようになります。

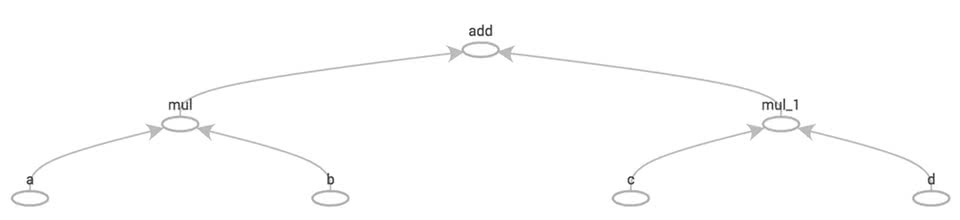
計算グラフ

こちらは、TensorFlowのTensorBoardで数式を実際に可視化してみた例です。 この数式(a \times b) + (c \times d) は、

  • 任意の変数a, b, c, d
  • 乗算が2つ
  • 加算が1つ

から成り立っています。 ノードが加算や乗算などの演算と初期値に対応し、エッジが計算結果の流れになります。

計算グラフの図をよく見ると、ノードは新しい変数と考えることができます。 元の数式は (a \times b) + (c \times d) ですが、

e = (a \times b)\\ f = (c \times d)

とすれば、一番上のノードと接続するノードの関係性を e + f と見ることができます。 グラフを構築することは、「計算グラフ上のノードに新しいシンボルを割り当てること」と言い換えることもできますね。

偏微分の計算

計算グラフ上で出力に対するシンボルの偏微分を計算する前に、少しだけ偏微分に関しておさらいしてみます。先程の数式上での f(a, b) = ab を各変数に関して偏微分してみると以下のようになります。

f(a,b) = a b \hspace{0.5in} \rightarrow \hspace{0.5in} \frac{\partial f}{\partial a} = b \hspace{0.5in} \frac{\partial f}{\partial b} = a

概念自体はそれほど難しくはなく、特定の変数以外を定数とみなして微分しているだけです。偏微分は、特定の１つの変数を微小変化させたときに、出力がどの程度変化するかを意味します。

同様に g(e, f) = e + f を各変数に関して偏微分してみます。

g(e,f) = e + f \hspace{0.5in} \rightarrow \hspace{0.5in} \frac{\partial g}{\partial e} = 1 \hspace{0.5in} \frac{\partial g}{\partial f} = 1

となります。こちらも偏微分する変数以外を定数とみなして微分しているだけですね。

損失関数の出力を f とすると、出力のすべてのパラメータに関する偏微分を計算すると、偏微分を並べたベクトルを定義することができます。このベクトル \nabla f = [\frac{\partial f}{\partial w_{1}}, ..., \frac{\partial f}{\partial w{i}}] を勾配と呼びます。

つまり、ニューラルネットワークの学習は、「損失関数の出力 f からネットワークのすべてのパラメータ w_{i} に関する偏微分 \frac{\partial f}{\partial w_i} を計算し、次に出力 f を勾配\\-\nabla f 方向に微小変化させるパラメータに変更することで、損失関数を0に近づけること」と直感的に理解することができます。

計算グラフ上での偏微分の計算

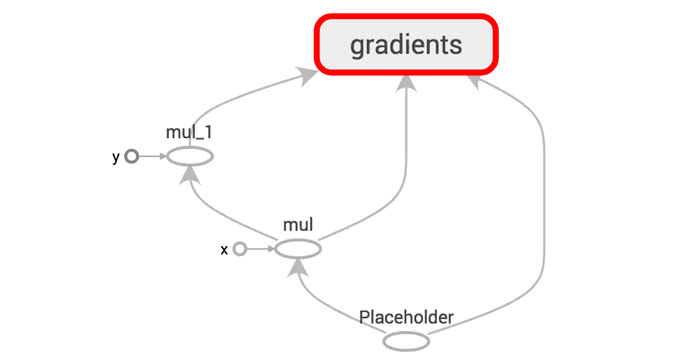
計算グラフ上では、どのように偏微分を計算すればいいのでしょうか。 計算グラフでは自動微分、その中でも特にリバースモード微分（トップダウン型自動微分）という方法をつかって各変数での出力に対する偏微分を求めていきます。

リバースモード微分は、１つの出力変数について、全ての中間変数に対する偏導関数値を計算していく手法で、以下の画像のように、出力の右側から左側に向かって「逆順に」偏導関数値を計算します。

具体的な数字を当てはめながら、実際に偏微分を計算してみます。例として

a = 3\\ b = 2\\ c = 4\\ d = 5

を計算グラフに割り当てて考えてみましょう。

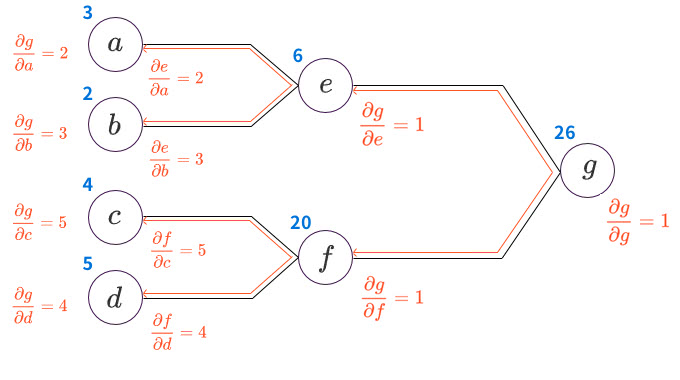
リバースモード微分

左から順に１つの入力値から偏導関数値を求めるフォワードモード微分（ボトムアップ型自動微分）では、すべてのノードで１つの変数に関する偏導関数値を得ることができますが、一方でリバースモード微分では、すべてのノードで出力値に関する偏導関数値を得ることができます。

リバースモード微分のメリットは、連鎖率を活かして出力値が少ない場合には、偏導関数値を高速に計算することができる点です。 上記の例では、左端の入力値に関する出力値の偏導関数値を得る場合に、以下のような計算をするだけで得られます。

\frac{\partial g}{\partial a} = \frac{\partial g}{\partial e} \frac{\partial e}{\partial a} = 2\\ \frac{\partial g}{\partial b} = \frac{\partial g}{\partial e} \frac{\partial e}{\partial b} = 3\\ \frac{\partial g}{\partial c} = \frac{\partial g}{\partial f} \frac{\partial f}{\partial c} = 5\\ \frac{\partial g}{\partial d} = \frac{\partial g}{\partial f} \frac{\partial f}{\partial d} = 4

途中で計算した \frac{\partial g}{\partial e} と \frac{\partial g}{\partial f} が再利用できている点に注目してください。 再利用しながら計算することで、リバースモードの場合は出力からパスを一巡するだけで出力値に対するすべての偏導関数値が得られるのです。

ニューラルネットワークの場合は、損失関数の出力が１つに対して、パラメータと入力値が非常に多いので、こちらのほうが高速に計算できます。

TensorFlowで実際に計算してみる

実際に以下のようなコードでTensorFlowに計算させることで、先程の計算を確かめてみます。TensorFlowには自動微分が実装されているので、簡単に勾配を求めることができます。

import tensorflow as tf

tf.reset_default_graph()
a = tf.placeholder(tf.float32, name='a')
b = tf.placeholder(tf.float32, name='b')
c = tf.placeholder(tf.float32, name='c')
d = tf.placeholder(tf.float32, name='d')
e = a * b
f = c * d
g = e + f
ga, gb, gc, gd, ge, gf = tf.gradients(g, [a, b, c, d, e, f])
feed_dict = {a: 3, b: 2, c: 4, d: 5}

with tf.Session() as sess:
  sess.run(tf.global_variables_initializer())
  # 青色の出力に向けた計算
  print(sess.run([a, b, c, d, e, f, g], feed_dict))
  # 赤色の勾配計算
  print(sess.run([ga, gb, gc, gd, ge, gf], feed_dict))

数値を計算するためにeとfのシンボルを割り当ててみましたが、コード上で省いても同じ計算グラフが構築されます。 出力は以下の通り、先程連鎖率で手計算した結果と同じ数値を得ることができました。

[array(3.0, dtype=float32), array(2.0, dtype=float32), array(4.0, dtype=float32), array(5.0, dtype=float32), 6.0, 20.0, 26.0]
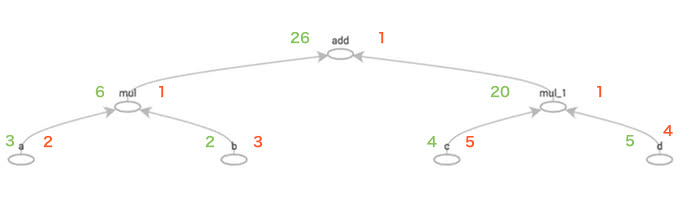
[2.0, 3.0, 5.0, 4.0, 1.0, 1.0]

実行してみると、下図のような計算グラフが構築されるはずです。 赤と緑で対応する勾配値と計算結果を書き込んでみました。

勾配計算

まとめ

本記事では、実際の具体例を見ながら、誤差逆伝播法のアルゴリズムを計算グラフを使って、できるだけ前提知識を減らしながらでも理解できるように解説してみました。

バックプロパゲーションは、最急降下法などのオプティマイザを理解する上でも、重要なテクニックです。

また、ニューラルネットワークの学習がうまくいかない場合に、原理上、偏微分を計算していることが分かっていればデバッグの足がかりになるはずです。

参考

[1] Automatic differentiation in machine learning: a survey
[2] Efficient Backprop