このページでは、NumPyのランダム配列生成方法をまとめていきます。 基本的にnumpy.randomのモジュールの中にある関数を使ってほとんどの乱数は生成できます。

一様な乱数を生成

一様乱数というのは、その範囲内においてある値が返される確率が全て均一な乱数のことです。

ここでは、randとrandintについて扱います。 randは[0, 1)(0以上1未満)の範囲で乱数を生成します。 もし[a, b)(a以上b未満)の範囲で乱数を生成したかったら、

 (b-a) * rand() + a

でできます。

randintは引数で指定された範囲(low, highにそれぞれ代入)における整数の乱数を返します。

In [1]: from numpy.random import * # NumPyのrandomモジュールの中の全ての関数をimport

In [2]: rand() # 何も値を設定しないと１つだけ値が返ってくる。
Out[2]: 0.008540556371092634

In [3]: randint(10) # 0~9の範囲にあるのランダムな整数を返す。
Out[3]: 8

In [4]: rand(2,3) # 2×3の乱数配列
Out[4]:
array([[ 0.58919258,  0.28724858,  0.15071801],
       [ 0.17489446,  0.35104423,  0.98827307]])

In [5]: randint(10, size =(2,3)) # size(デフォルトはNone)に配列の形を代入する。
Out[5]:
array([[3, 9, 2],
       [5, 4, 1]])

In [6]: randint(5,10, size = 10) # 5以上10"未満"の範囲でのランダムな整数を返す。
Out[6]: array([9, 5, 5, 8, 6, 9, 5, 9, 7, 6])

In [7]: (10-5)*rand(10) + 5  # 5以上10"未満""の範囲でランダムな実数を返す。
Out[7]:
array([ 8.62241919,  5.07799317,  8.05223236,  7.91501649,  8.1365352 ,
        5.19681854,  9.57140438,  6.18058095,  9.66216214,  5.43703069])

生成した乱数を固定する。

seed機能を使えば、生成した乱数を固定することができます。プログラムが正しく機能しているか確かめているときなどの、生成した乱数にも再現性が必要なときによく使われます。

In [1]: from numpy.random import *

In [2]: seed(seed = 21) # シードを 21　に設定

In [3]: rand() # 乱数を１つ生成
Out[3]: 0.04872488080912729

In [4]: seed(21)  # もう一度シードを21に設定（引数でseedを選択しなくてもシードは設定できます。）

In [5]: rand()  # 同じ値が返されます。
Out[5]: 0.04872488080912729

In [6]: seed(10) # 配列でも同じことができます。

In [7]: rand(20) # シードを10に設定して、乱数を２０個生成。
Out[7]:
array([ 0.77132064,  0.02075195,  0.63364823,  0.74880388,  0.49850701,
        0.22479665,  0.19806286,  0.76053071,  0.16911084,  0.08833981,
        0.68535982,  0.95339335,  0.00394827,  0.51219226,  0.81262096,
        0.61252607,  0.72175532,  0.29187607,  0.91777412,  0.71457578])

In [8]: seed(23) # シードを23　に設定して、乱数を２０個生成。

In [9]: rand(20)
Out[9]:
array([ 0.51729788,  0.9469626 ,  0.76545976,  0.28239584,  0.22104536,
        0.68622209,  0.1671392 ,  0.39244247,  0.61805235,  0.41193009,
        0.00246488,  0.88403218,  0.88494754,  0.30040969,  0.58958187,
        0.97842692,  0.84509382,  0.06507544,  0.29474446,  0.28793444])

In [10]: seed(10) # また10に戻して確認。

In [11]: rand(20) # 同じ値が返ってきてる。
Out[11]:
array([ 0.77132064,  0.02075195,  0.63364823,  0.74880388,  0.49850701,
        0.22479665,  0.19806286,  0.76053071,  0.16911084,  0.08833981,
        0.68535982,  0.95339335,  0.00394827,  0.51219226,  0.81262096,
        0.61252607,  0.72175532,  0.29187607,  0.91777412,  0.71457578])

In [12]: seed(23) # 23でも同様に

In [13]: rand(20) # 同じ値が返ってくる。
Out[13]:
array([ 0.51729788,  0.9469626 ,  0.76545976,  0.28239584,  0.22104536,
        0.68622209,  0.1671392 ,  0.39244247,  0.61805235,  0.41193009,
        0.00246488,  0.88403218,  0.88494754,  0.30040969,  0.58958187,
        0.97842692,  0.84509382,  0.06507544,  0.29474446,  0.28793444])

リストからのランダムな抽出、リストのシャッフル

あらかじめ作られたリストからランダムに要素を抽出したり、リストに書かれているものの順番をランダムに入れ替えることについて扱っていきます。

ランダムに抽出する。

これには、choiceを使います。 この関数は、与えられたリストからランダムに要素を抽出できるだけでなく、その抽出の仕方に重みをつけたり、重複のあるなしを選択したりすることができます。

In [1]: from numpy.random import *

In [2]: a = ['Python', 'Ruby', 'Java', 'JavaScript', 'PHP'] #　リストを１つ作成

In [3]: choice(a, 3)  # aから３つの要素をランダムに取り出す。
Out[3]:
array(['Python', 'Java', 'Ruby'],
      dtype='<U10')

In [4]: choice(a, 5, replace = False) # 重複なしで取り出し。
Out[4]:
array(['Python', 'Java', 'Ruby', 'PHP', 'JavaScript'],
      dtype='<U10')

In [5]: choice(a, 20, p = [0.8, 0.05, 0.05, 0.05, 0.05]) # pにリストを渡すことで取り出す値の頻度を変える。pの値の合計は 1 になることに注意。
Out[5]:
array(['Python', 'Python', 'Python', 'Python', 'Python', 'Python',
       'Python', 'Python', 'Python', 'Python', 'Python', 'Python',
       'Python', 'Python', 'Python', 'Python', 'Python', 'Python', 'Ruby',
       'Python'],  
      dtype='<U10')             # Pythonに比重を高く置いたので、Pythonが頻出しているリストが返ってきた。

In [6]: choice(5, 10) # 最初の引数に整数をわたすと、np.arange(5)で生成されるリストが渡されることと同じことになる。この場合はでは、5未満0以上の整数をランダムに10個生成する。
Out[6]: array([1, 2, 4, 3, 4, 0, 3, 2, 0, 4])

リストのシャッフル

shuffleが使えるとよいでしょう。 ただ、リストの順番をランダムに入れ替えるだけです。 新しいリストが作成されるわけではなく、リストの中身が変更されるので、注意してください。

In [1]: import numpy as np

In [2]: from numpy.random import *

In [3]: a = np.arange(10)

In [4]: a
Out[4]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

In [5]: shuffle(a)  # aの要素の順番をランダムに入れ替える。

In [6]: a      # aの中身を確かめる。
Out[6]: array([5, 0, 9, 3, 6, 8, 4, 1, 2, 7])

特定の確率分布に従った乱数の生成

統計学などでよく使われている正規分布や、二項分布に従う乱数を生成していきます。

正規分布に従った乱数の生成

正規分布は、

{\large f(x) = \frac{1}{\sqrt{2\pi}\sigma}\exp\Bigl(-\frac{(x-\mu)^{2}}{2\sigma^{2}}\Bigr)} \\ \sigma = {\Large 標準偏差}　\ \mu = {\Large 平均} \

上記の確率密度関数 f(x) \\\\ に従った分布のことをいいます。

*参考 アタリマエ！　正規分布とは何なのか？その基本的な性質と理解するコツをを書いていきます

この中で、特に \sigma = 1, \mu = 0 \\\\ となっているものを標準正規分布と呼びます。 標準正規分布を使いたい場合はrandnを、他の正規分布が使いたいときはnormalを使って引数でそれぞれ平均(loc)、標準偏差(scale)を指定して実行すれば求める分布になります。また、normalのデフォルトの値は、標準正規分布のものになっているのでsizeで配列の形を指定してやれば、randnと同じ使い方ができます。

In [1]: from numpy.random import *

In [2]: randn()  #　何も引数を入れないと1つだけ返す。
Out[2]: -1.3305467786751202

In [3]: normal()  # これも同様。
Out[3]: -0.9027907174237491

In [4]: randn(10)  # 1次元配列
Out[4]:
array([ 0.33530916, -0.37144931, -0.10819173, -1.10083762, -0.19231432,
       -0.23810618,  1.3522678 ,  0.01818202,  0.07467403,  1.0657649 ])

In [5]: normal(loc = 1,scale =  2.0, size = 10) # locは平均、scaleは標準偏差、sizeは返す配列の形。
Out[5]:
array([ 4.44090839, -0.58686905,  0.87943739,  1.17504152, -0.71920899,
       -1.7246826 , -0.10957232, -2.27397748,  2.4768217 , -2.43637281])

In [6]: normal(size = 10) # randn(10)と同様に標準正規分布（ガウス分布）でランダムな数値を出力する
Out[6]:
array([ 0.02474026, -0.29251229,  0.36310153,  0.73227268, -0.98166425,
       -0.72832843, -0.64461233,  1.22547922, -0.81135131, -1.062154  ])

二項分布に従った乱数の生成

これにはbinomialを使います。 二項分布は

{\large P(n) = \begin{eqnarray}{}_n C _k \end{eqnarray}p^{k}(1-p)^{n-k}} \\

に従った分布のことをいいます。

n,p \\\\

がパラメータとなっており、統計学においてはそれぞれ、試行の回数、事象の起こる確率として設定されることが多いです。また、\begin{eqnarray}{}_n C _k \end{eqnarray} \\\\　 は組み合わせの数を表しており、

\begin{eqnarray}{}_n C _k \end{eqnarray} = \frac{n!}{k!(n-k)!} \\

で計算できます。

*参考 アタリマエ！　コイン投げから分かる二項分布。正規分布やポアソン分布との関係性と近似について

引数は(n, p, size)となっており、sizeのデフォルト値がNoneとなっています。

In [1]: from numpy.random import *

In [2]: binomial(100, 0.5, 30) # (n, p) = (100, 0.5)での事象が起こる回数。これを30回やったとすると。
Out[2]:
array([53, 45, 42, 50, 55, 43, 48, 47, 51, 44, 53, 42, 46, 42, 50, 58, 47,
       48, 46, 41, 50, 40, 41, 51, 48, 54, 42, 50, 45, 53])

ベータ分布に従った乱数の生成

これにはbetaを使います。 ベータ分布は、

{\large f(x) = \frac{x^{\alpha - 1}(1-x)^{\beta - 1}}{B(\alpha,\beta)}} \\ {\small B(\alpha,\beta) = \int_{1}^{0}x^{\alpha-1}(1-x)^{\beta-1}dx} \\ \alpha, \beta は パラメータ

で表される確率密度関数f(x) \\\\に従った分布で、x \\\\ の範囲は 0\leqq{x}\leqq1 \\\\　で与えらます。

*参考 コインで理解するベータ分布

In [1]: from numpy.random import *

In [2]: beta(1, 2, size = 10) # (α, β) = (1,2)　となるベータ分布に基づく乱数を10個生成。
Out[2]:
array([ 0.09632812,  0.42630832,  0.24711994,  0.0310272 ,  0.20418792,
        0.11835707,  0.09927322,  0.87275003,  0.59023081,  0.87157062])

ガンマ分布に従った乱数の生成

これにはgammaを使います。 ガンマ分布とは、

{\large f(x) = x^{n-1}\frac{e^{-\frac{x}{\beta}}}{\Gamma(\alpha)\beta^{\alpha}}} \\ \alpha, \beta　は　正のパラメータ。\\

で表されるf(x) \\\\に従った分布のことをいいます。 確率\frac{1}{\beta} \\\\で起こる事象が\alpha \\\\回起こるまでの時間を表しています。 ここで用いられる \Gamma(\alpha) \\\\ はガンマ関数と呼ばれるものです。

*参考 高校数学の美しい物語　ガンマ関数の定義と性質

引数は(shape, scale, size)　となっており、shapeは\alpha \\\\,scaleは\beta \\\\に対応しています。sizeは例のごとく、返す配列の形を指定します。

In [1]: from numpy.random import *

In [2]: gamma(2, 2, size = 10) # (shape, scale) = (α, β) = (2,2)　における乱数を生成。
Out[2]:
array([ 8.10374089,  3.69483207,  4.36710089,  6.67415716,  3.82689173,
        0.24621911,  3.35644722,  3.28627308,  2.20573852,  0.43484218])

ポアソン分布に従った乱数の生成

これにはpoissonを使います。 ポアソン分布は、

P(k) = e^{-\lambda}\frac{\lambda^{k}}{k!}

に従った確率分布のことをいいます。これは、ある一定期間の間に平均\lambda \\\\回起こるような事象がその期間の中でk \\\\回起こる確率を示しています。

*参考 高校数学の美しい物語　ポアソン分布の意味と平均・分散

この関数は、引数で\lambda \\\\ と、sizeだけ指定します。

In [1]: from numpy.random import *

In [2]: poisson(2, 10) # λ =2, size = 10　のランダム配列生成。
Out[2]: array([4, 4, 2, 0, 2, 6, 4, 3, 0, 2])

In [3]: poisson(2, (2,2)) #　２次元配列もできます。
Out[3]:
array([[0, 1],
       [2, 5]])

カイ二乗分布に従った乱数の生成

これにはchisquareを使います。 カイ二乗分布というのは、標準正規分布に従った乱数の二乗をいくつか足したものをいいます。足していく個数というのは、自由度k \\\\で決まります。

{\large Z = \sum_{i=1}^{k}X_i} \\ {\normalsize X_i}　{\large は標準正規分布に従う独立の乱数。} \\

このZ \\\\の分布がカイ二乗分布になります。 少し説明が分かりにくいと思うので、分かりやすく紹介しているサイトのリンクをはっておきます。

*参考

χ2（カイ２乗）分布

【統計学】正規分布とカイ二乗分布の関係を可視化してみる。

In [1]: from numpy.random import *

In [2]: chisquare(2, 10) # 自由度2で10個の値を生成。
Out[2]:
array([ 0.81317002,  0.10309116,  2.75306747,  5.00138087,  1.05388799,
        0.92378472,  6.76553474,  0.69259463,  0.41571649,  1.15612406])

ヒストグラムを使った分布の確認

生成した乱数が、自分のほしい分布に従っているか確認したいときは、matplotlibを使ってヒストグラムを出すとわかりやすいです。randnが標準正規分布に従っているか、確かめてみます。 確認のため、標準正規分布に従った確率密度関数のグラフも一緒に確認してみます。 また、確率密度関数を記述する上で、numpyの関数を一部使用しています。これについての詳しい解説はまた別のページで行う予定です。

In [1]: import numpy as np
In [2]: from matplotlib import pyplot as plt
In [3]: def standard_normal_distribution(x):
          return (1/np.sqrt(2*np.pi))*np.exp(-x**2/2)*1000 # 標準正規分布の確率密度関数を1000倍に拡大。(ヒストグラムの度数の幅が0.01なため、データ数の1/100倍だけ拡大)
In [4]: a = np.random.randn(100000) # 10万個の標準正規分布に従った乱数を生成。
In [5]: fig = plt.figure()
In [6]: ax = fig.add_subplot(1,1,1)
In [7]: x = np.linspace(-5, 5, 1000)
In [8]: ax.hist(a, bins = 1000)
In [9]: ax.plot(x, standard_normal_distribution(x))
In [10]: fig.show()

出力されたグラフはこんな感じになります。 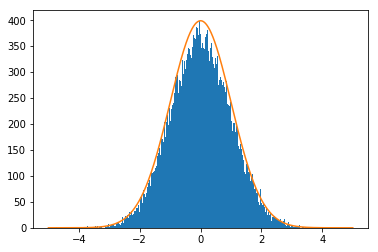標準正規分布 きれいな形の標準正規分布になっていますね。