今回は、機械学習の中でも機械が自ら答えを模索していく強化学習について扱っていきます。

今回はQ学習と方策勾配法と呼ばれる2つをNumPyで実装していきましょう。Q学習の詳しい実装は以下の記事でされているので本記事ではQ学習の解説と方策勾配法の解説と実装とをメインに扱っていきます。

強化学習の基本的な考え方もこの記事に掲載されていますので是非１度目を通してからこの記事を見ることをおすすめします。

これさえ読めばすぐに理解できる強化学習の導入と実践 /machine_learning/2017/08/10/reinforcement-learning.html

OpenAI Gymとは

OpenAIと言われる団体が作った、強化学習を試すためのプラットフォームです。この中には様々なゲームが内包され、Python上で簡単に実行できるようになっています。OpenAI Gymはメンテナンスされなくなってしまったため、Gymnasiumというフォークされたプロジェクトを使用します。

今回の強化学習では、その中でCartPoleを扱っていきたいと思います。

CartPole

CartPoleは台座の上に連結されている棒を倒さないように台座を左右に押していくゲーム内容となっています。一定の角度以上棒(Pole)が倒れてしまうとゲームオーバーです。

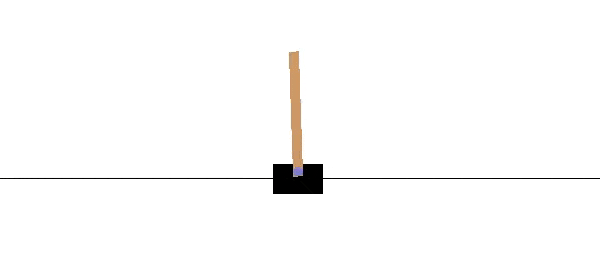
ゲーム画面は以上のようになっています。

実際は、1(台座を右に押す)か0(左に押す)を入力していき、その都度台座(カート)の位置や速度、棒（ポール）の角度と速度が環境変数として返されます。概要は以下のとおりです。

状態

環境から出力される状態 s は以下の表の4つの変数からなります。

番号 名前 最小値 最大値
0 カートの位置 -2.4 2.4
1 カートの速度 -inf inf
2 ポールの角度 -41.8° 41.8°
3 ポールの速度 -inf inf

行動

ある状態s からとりうる行動A(s) は以下の2つになります。

番号 名前
0 左にカートを押す
1 右にカートを押す

報酬

報酬はポールが倒れない限り1タイムステップ毎に1得られます。

インストールからゲームの実行まで

まずはGymnasiumをインストールしましょう。
以下のコマンドを実行すれば基本パッケージはインストールされます。

$ pip install gymnasium pygame

では次にPythonのインタプリタを起動していきます。
gymをインポート

import gymnasium as gym
env = gym.make('CartPole-v1', render_mode='human') # ゲームの状態を描画しない場合はrender_mode=Noneとする

状態の初期化

observation, info = env.reset()

CartPoleで利用者がとれる行動は右に押す(1)か左に押す(0)かなのでこれをactionという変数に入れてゲームを実行してみます。

action = 1 # とりあえず右に押して見る
observation, reward, terminated, truncated, info = env.step(action) # stepを実行すると行動を起こした直後の状態、報酬、ゲームが終了したかどうか、打ち切り（時間切れ）、情報の5つの変数が返される

これは各ステップごとに実行しないと様子が動いていかないので注意してください。
では簡単に実行してみましょう。

import numpy as np
observation, info = env.reset()

for k in range(100):
    observation, reward, terminated, truncated, info = env.step(np.random.randint(1))
    if terminated: # 終了シグナルでループを出る
        break
    env.close()

実行するとすぐに終了してしまうのが分かると思います。gymansiumのCartPole-v1では角度が12°以上左右どちらかに倒れるか、画面半分以上進むとゲームオーバーになってしまいます。 これをこれから学習させて棒が倒れないように台座を動かす方法を習得していきます。

Q学習

Q学習とは

Q学習(Q-learning)とは、状態(s)のときにとる行動(a)によってどの程度の価値があるのかを 示す価値関数Q(s,a)があり、この関数を学習させていきます。
この価値関数がより高い値になる行動を選んでいけばよいというのがこのQ学習の考え方です。
(学習を進める関係上ある程度ランダムな行動を挟んだほうがよいと言われています。この手法を\epsilon -グリーディー法と呼びます。)

Q学習の最も基本的なモデルではこの価値関数の値をテーブルを使って表していきます。
例えば10個の状態があってそれぞれに２個ずつ行動の選択肢が存在するとすると 10×２のテーブルでこの価値関数を表現することができるわけです。

今回は4つある状態変数をそれぞれ4つに区分していくので状態の全てが4^4 = 256 通りに分類することができます。
その256通りの状態の中で右に押す場合、左に押す場合それぞれにおける価値を更新していきます。

これらの価値関数の更新は通常以下の式によってなされます。

Q(s_t, a_t) \gets (1-\alpha)Q(s_t, a_t) + \alpha(r_{t+1} + \gamma max_{a_{t+1}}Q(s_{t+1}, a_{t+1}))

次の状態の価値観数の中で最大となるものに減衰係数\gamma をつけ、次の状態で得られた報酬r_{t+1} を足し合わせたものをある一定の比率\alpha で足し合わせることで更新されます。

では、実際の実装を見ていきましょう。コード自体は先程リンクを掲載した記事に載っているものですが、それにコメントを加えています。

アルゴリズムの考え方自体は記事を読んでもらえればよくわかると思いますのでそちらに譲ります。

以下のコードをcartpole.pyなどの名前で保存し、

$ python cartpole.py

で実行することができます。

import gymnasium as gym
import numpy as np

env = gym.make("CartPole-v1", render_mode='human') # 描画しない場合はrender_mode=Noneにする

goal_average_steps = 195 # 195ステップ連続でポールが倒れないことを目指す
max_number_of_steps = 200 # 最大ステップ数
num_consecutive_iterations = 100 # 評価の範囲のエピソード数
num_episodes = 5000
last_time_steps = np.zeros(num_consecutive_iterations)

q_table = np.random.uniform(low=-1, high=1, size=(4**4, env.action_space.n))

def bins(clip_min, clip_max, num):
    return np.linspace(clip_min, clip_max, num + 1)[1:-1]
# np.linspaceは指定された範囲における等間隔数列を返す。

def digitize_state(observation):
# 各値を４個の離散値に変換
# np.digitizeは与えられた値をbinsで指定した基数に当てはめる関数。インデックスを返す。
    cart_pos, cart_v, pole_angle, pole_v = observation
    digitized = [np.digitize(cart_pos, bins=bins(-2.4, 2.4, 4)),
    np.digitize(cart_v, bins = bins(-3.0, 3.0, 4)),
    np.digitize(pole_angle, bins=bins(-0.2095, 0.2095, 4)),
    np.digitize(pole_v, bins=bins(-2.0, 2.0, 4))]

# 0~255に変換
    return sum([x* (4**i) for i, x in enumerate(digitized)]) # インデックス付きループをすることができる。


def get_action(state, action, observation, reward, episode):
    next_state = digitize_state(observation)

    epsilon = 0.5 * (0.99 ** episode)
    if epsilon <= np.random.uniform(0, 1): # もし一様乱数が0.2以上であれば
        next_action = np.argmax(q_table[next_state])# q_tableの中で次に取りうる行動の中で最も価値の高いものを
# next_actionに格納する
    else:# 反対に20%の確率でランダムな行動を取る
        next_action = np.random.choice([0, 1])


    # Qテーブルの更新
    alpha = 0.2
    gamma = 0.99
    q_table[state, action] = (1 - alpha) * q_table[state, action] + \
    alpha * (reward + gamma * q_table[next_state, next_action])
    return next_action, next_state

step_list = []
for episode in range(num_episodes):
    # 環境の初期化
    observation, info = env.reset()

    state = digitize_state(observation)
    action = np.argmax(q_table[state])

    episode_reward = 0
    for t in range(max_number_of_steps):
        observation, reward, terminated, truncated, info = env.step(action) # actionを取ったときの環境、報酬、状態が終わったかどうか、打ち切り（時間切れ）、デバッグに有益な情報
        if terminated or truncated:
            reward = -200

        action, state = get_action(state, action, observation, reward, episode)
        episode_reward += reward

        if terminated or truncated or t == max_number_of_steps - 1:
            print(f'{episode} finished after {t + 1} time steps / mean {last_time_steps.mean()}')
            last_time_steps = np.hstack((last_time_steps[1:], [t+1])) # 継続したステップ数をステップのリストの最後に加える。np.hstack関数は配列をつなげる関数。
            step_list.append(t+1)
            break

    if (last_time_steps.mean() >= goal_average_steps): # 直近の100エピソードの平均が195以上であれば成功
        print('Episode %d train agent successfully!' % episode)
        break


# ステップ数の推移を描画
import matplotlib.pyplot as plt
plt.plot(step_list)
plt.xlabel('episode')
plt.ylabel('mean_step')
plt.show()

この実行結果は以下のようになりました。

紹介していない関数があったので紹介します。 連続値を離散値に格納する関数np.digitizeです。これのAPIドキュメントは以下のとおりです。

numpy.digitize(x, bins, right=False)

params:

パラメータ名 型 概要
x 配列に相当するもの 基数に当てはめたい値（もしくは値が格納されている配列）を指定します。
bins 1次元配列 基数(bins)の配列を指定します。
right bool値 (省略可能)初期値False
右端と左端どちらを範囲に含むかを指定します。デフォルトでは右端を含まない(right==False)ようになっています。

returns:

xと同じ形状でそれぞれの値が格納される基数のインデックスを返します。

方策勾配法

次は方策勾配法で同じ問題を解いていきます。

この方法はいくつかのエピソードごとにパラメータを更新していくものでニューラルネットワークと組み合わせてよく使われます（1エピソード毎ではなくいくつかのエピソードをバッチとしてそれらの情報を用いて更新する場合がほとんどです）。

設定された報酬関数の値を最大化するようにネットワークを学習させていくものです。教師あり学習では損失関数を使っていましたが、今回理想とする状態というのがわからない状態ですのでその状態がどれだけ良いものなのかを評価する報酬関数で代用しますがそれ以外の基本的な考え方は教師あり学習とほとんど変わりません。

今回は右に押す確率をobservationで得られた４つのパラメータ（カートの位置、カートの速度、ポールの角度、ポールの速度）を使って学習させていきたいと思います。

今回使っていく報酬はかなりシンプルなものです。1エピソードにおいていくつのステップ耐えることができたかをステップ数で記録し、それが200以上であれば報酬は-1、200を超えなければそのエピソードにおけるステップ数から200を引くという実装にしました。

なのでsエピソード目の報酬R_s \\\\ は以下のようになります。

R_t = \begin{cases} -1 (エピソード数 \geq 200) \\ エピソード数-200 ( エピソード数 < 200) \end{cases}

今回は扱わない報酬ですが、よく使われる報酬関数の与え方を紹介します。そのステップにおける報酬r_t と、これに減衰率\gamma をかけ合わせたnステップ先における報酬\gamma^n r_{t+n} を足していきます。

ステップ自体の報酬はステップ数が基本ですがポールが倒れた場合(terminatedがTrueになるとき)は報酬をかなり小さいものにします(Q学習だと-200にしました)。

具体的には以下のR_t がそのステップにおける報酬ということになります。

R_t = \sum_{n=0}^{N} \gamma^n r_{t+n}

学習の進め方

それぞれのパラメーターWを偏微分を使って更新していきます。

出力p(x)(コードの中では関数calculate(X, w)の返り値)、報酬をR_t とすると

W \gets W + \eta \frac{R_t}{\partial W}

誤差逆伝播法を用いて計算しています。

ここでの\eta は学習率です。このあたりの詳しい解説はニューラルネットワークの実装の部分で行っているのでそちらの方を参考にしてください。今回損失関数ではなく報酬を最大化するために学習をすすめていくため、パラメーターに対して偏微分の値を引く のではなく 足す ということ以外はやってることは変わりません。

実装上では、予め値をずらした状態でエピソードを進行させ、そのずらした分をパラメーター自身の偏差として扱っています。

NumPyでニューラルネットワークを実装してみる　理論編/features/numpy-neuralnetwork-2.html

NumPyでニューラルネットワークを実装してみる　多層化と誤差逆伝播法 /features/numpy-neuralnetwork-4.html

では簡単に実装していきましょう。今回はバイアスにあたるパラメーターbは使わないでシンプルなものを使って実装していきます。

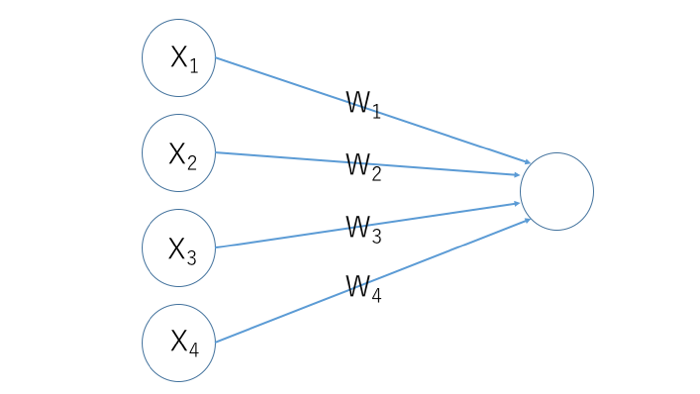
ニューラルネットワークは中間層なしの単層構造です。活性化関数は使わず、最後の値が0を超えていれば右に押し、0を超えなければ左に押すというシンプルな手法で試してみます。

import gymnasium as gym
import numpy as np
import matplotlib.pyplot as plt

def do_episode(w, env):
    terminated = False
    observation, info = env.reset()
    num_steps = 0

    while not terminated and num_steps <= max_number_of_steps:
        action = take_action(observation, w)
        observation, reward, terminated, truncated, info = env.step(action)
        num_steps += 1
    # ここで報酬を与える。基本的に(連続したステップ数)-(最大ステップ数)で与えられる。
    step_val = -1 if num_steps >= max_number_of_steps else num_steps - max_number_of_steps
    return step_val, num_steps

def take_action(X, w): # 値が0を超えたら1を返すようにする
    action = 1 if calculate(X, w) > 0.0 else 0
    return action

def calculate(X, w):
    result = np.dot(X, w) # 返り値は配列ではなく、１つの値になる。
    return result

env = gym.make("CartPole-v1", render_mode=None) # 描画する場合はrender_mode='human'にする

eta = 0.2
sigma = 0.05 # パラメーターを変動させる値の標準偏差

max_episodes = 5000 # 学習を行う最大エピソード数
max_number_of_steps = 200
n_states = 4 # 入力のパラメーター数
num_batch = 10
num_consecutive_iterations = 100 # 評価の範囲のエピソード数

w = np.random.randn(n_states)
reward_list = np.zeros(num_batch)
last_time_steps = np.zeros(num_consecutive_iterations)
mean_list = [] # 学習の進行具合を過去100エピソードのステップ数の平均で記録する

for episode in range(max_episodes // num_batch):
    N = np.random.normal(scale=sigma, size=(num_batch, w.shape[0]))
    # パラメーターの値を変動させるための値。これが偏差になる。

    for i in range(num_batch):
        w_try = w + N[i]
        reward, steps = do_episode(w_try, env)
        if i == num_batch-1:
            print(f'{episode*num_batch} Episode finished after {steps} steps / mean {last_time_steps.mean()}')
        last_time_steps = np.hstack((last_time_steps[1:], [steps]))
        reward_list[i] = reward
        mean_list.append(last_time_steps.mean())
    if last_time_steps.mean() >= 195: break # 平均が195以上であれば学習終了

    std = np.std(reward_list)
    if std == 0: std = 1
    # 報酬の値を正規化する
    A = (reward_list - np.mean(reward_list)) / std
    # ここでパラメーターの更新を行う
    w_delta = eta / (num_batch * sigma) * np.dot(N.T, A)
    # 振れ幅を調整するためにsigmaをかけている。
    w += w_delta

env.close()
# グラフの表示

plt.plot(mean_list)
plt.xlabel('episode')
plt.ylabel('mean_step')
plt.show()

これの実行結果は以下のようになります。

0 Episode finished after 9 steps / mean 1.040000
10 Episode finished after 14 steps / mean 2.180000
20 Episode finished after 14 steps / mean 4.200000
30 Episode finished after 50 steps / mean 5.980000
40 Episode finished after 15 steps / mean 8.170000
50 Episode finished after 20 steps / mean 10.270000
60 Episode finished after 22 steps / mean 12.870000
70 Episode finished after 22 steps / mean 15.620000
80 Episode finished after 16 steps / mean 18.620000
90 Episode finished after 20 steps / mean 21.470000
100 Episode finished after 21 steps / mean 22.820000
110 Episode finished after 14 steps / mean 23.560000
120 Episode finished after 12 steps / mean 23.720000
130 Episode finished after 19 steps / mean 24.260000
140 Episode finished after 26 steps / mean 25.190000
150 Episode finished after 30 steps / mean 26.440000
160 Episode finished after 28 steps / mean 26.570000
170 Episode finished after 23 steps / mean 26.950000
180 Episode finished after 35 steps / mean 27.380000
190 Episode finished after 22 steps / mean 27.900000
200 Episode finished after 69 steps / mean 29.050000

・
・
・

1400 Episode finished after 200 steps / mean 180.730000
1410 Episode finished after 200 steps / mean 181.270000
1420 Episode finished after 200 steps / mean 183.190000
1430 Episode finished after 200 steps / mean 184.720000
1440 Episode finished after 200 steps / mean 190.020000
1450 Episode finished after 200 steps / mean 190.780000
1460 Episode finished after 200 steps / mean 191.850000
1470 Episode finished after 200 steps / mean 194.050000
1480 Episode finished after 200 steps / mean 195.750000

これをグラフで示すと以下のようになります。

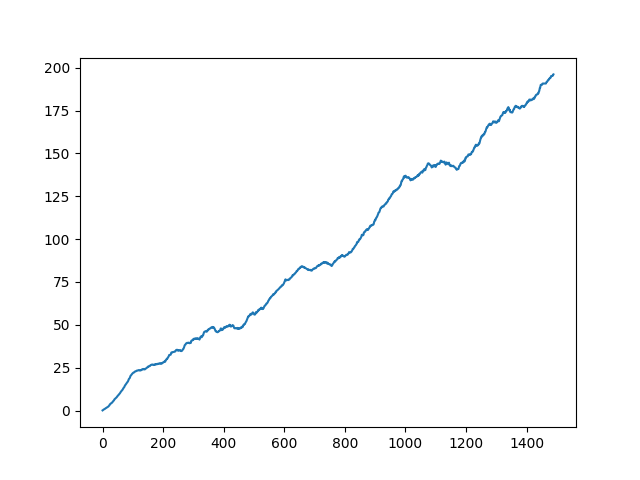うまく学習できました。 20エピソードあるバッチを1000回繰り返すのが最大ですが、2000エピソード以内には収束します。

まとめ

今回はNumPyを使って強化学習の問題に取り組みました。

この記事では代表的な手法であるQ学習と方策勾配法を扱いましたが、他にも色々な手法があったり違う実装の仕方も多数存在します。

是非自分なりに実装して色々試してみてください。

参考