今回はニューラルネットワークをNumPyで実装するシリーズの2回目です。いよいよニューラルネットワークの理論について学んでみましょう。

理論的な背景を知ることで、今後の納得感が変わってくるはずです。

まずは最もシンプルな構造について学びます。

ニューラルネットワーク

前回は、脳内の認知メカニズムをざっくりとまとめました。それではこの章からは機械学習の分野で実際に使われているニューラルネットワークについて詳しく見ていきます。

ニューラルネットワークは、先程１章で紹介した脳における神経細胞の情報伝達の仕組みを模倣したものです。

神経細胞の模倣

では、先程学んだ内容を基に神経細胞の情報伝達の仕組みをモデル化していきましょう。 ここで１つ１つの神経細胞を表現しグラフのノードのように見ます。そしてそれぞれの神経細胞をエッジでつなぎます。

神経細胞

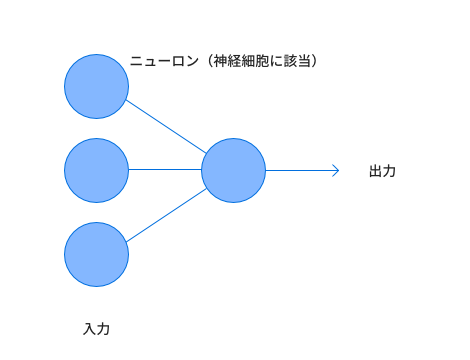
そこで信号を受け取ったニューロンが発火するための条件と発火した際に与える信号を考えます。まずそれぞれのニューロンから入力される値をx_1, x_2, x_3 とします。この３つの値を受け取ったニューロンから出力される値をy とします。

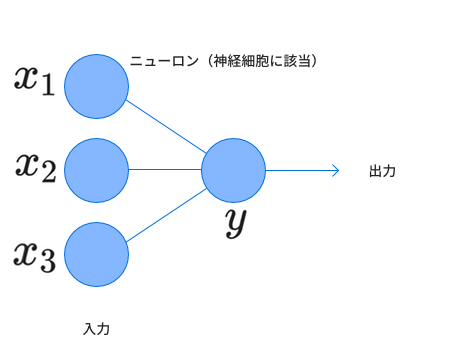
神経細胞2

このとき、ある値b を超えた時はb を超えた分だけの値を出力し、それ以外のときは０を出力するものをy とします。 ここにおけるb は実際の神経細胞における活性電位（発火するために必要な電位）と見ることができます。実際は信号の強さを表す際、脳の神経細胞では発火の回数で表すのですが今回はそれを値の大きさで代用することにします。

応答の様子は実験の結果よりシグモイド関数に形がよく似ていることが知られています。（ラットの実験の文献しか見つけられませんでした。筆者はどこかでそのような文面を読んだ記憶があるのですが出典を探せず申し訳ありません。)

なので、ここでもシグモイド関数を使ってそれを真似してみましょう。

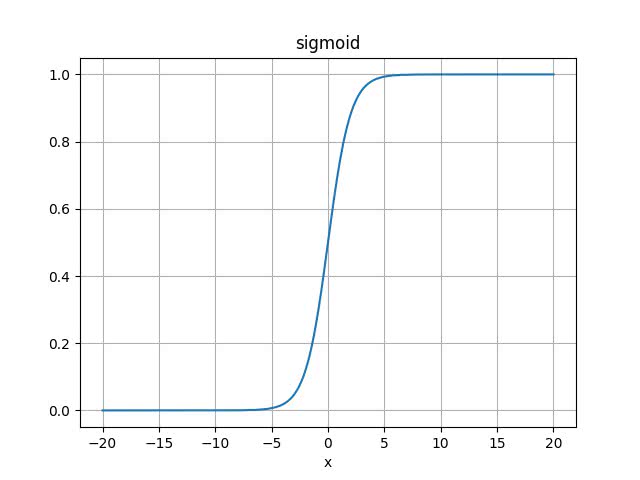
シグモイド関数は以下のように表されます。

\sigma(x) \equiv \frac{1}{1+exp(-x)}

これをグラフにプロットすると、以下の図のようになります。

なので、先程のニューロンモデルにこれを適用すると、

y = \sigma(x_1 + x_2 + x_3) \\ \sigma(x) = \frac{1}{1+exp(-x)}

となります。

今回扱うモデルでシグモイド関数のように入力された値に対するニューロンの出力の特性を決める関数を 活性化関数と呼びます。

パラメーターの導入

これでニューラルネットワークの基本構造を理解しました。しかし我々が行いたいのはこれを使って何かしらの学習させることです。

となると、学習の過程で変化する部分が欲しいですね。この状態ですと入力x_1, x_2, x_3 は学習の際は固定された値とみなすことができ、何も変化が起こらないのです。

そこで、これらの入力値に重みを加え、その重みを調整してあげることで学習を進めていくことにしましょう。 また、シグモイド関数の基準点は０にありますがそこに合わせるという意味でバイアスを入力の和に加えることにします。

この2種類のパラメーターを調整していくことにします。

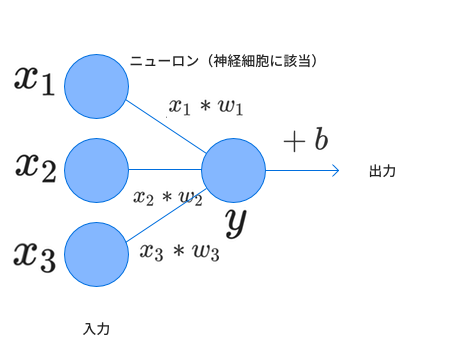
ニューロンの計算

従って、出力 y は

y = \sigma(x_1*w_1 + x_2*w_2 + x_3*w_3 + b)

となります。これをベクトルに書き換えて、\vec{x} = (x_1, x_2, x_3)^T, \vec{w} = (w_1, w_2, w_3)^T とすると、内積の形で表すことができ、

y = \sigma(\vec{x} \cdot \vec{w} + b)

となります。

これがニューラルネットワークの基本形となります。次は、このパラメータを学習させていきたいと思います。

損失関数の設定

それでは学習を始めていきますと言いたいところですが、もう1つ準備が必要です。

それは、学習がうまく進んだ理想の状態からどれだけ離れているのかを示そうとして我々が勝手に設定する関数です。一般的に損失関数と呼ばれています。

入力ベクトル\vec{x}^n に対して目標とする値をt_n と表現します。

まず最初に思いつく損失関数は何でしょうか。２節まででニューラルネットワークの最も基本的なモデルを学んでいます。その出力とt_n との差をとってそれを合計するというのがまず思いつきますね。

なので損失関数をLとすると、

L = \sum_{n=1}^{N}||t_n - y(\vec{x}^n)||

通常学習をするときは、１つの入力と目標値のセットだけでなく複数のセット（今回はN個のセットを使うとしました）を用いて行います。なのでそれらを合計したものを損失関数としています。

これでも問題ありませんが、このあとに行う学習を見越していくと以下の式のように差の2乗和がよく使われます。

L = \frac{1}{2N}\sum_{n=1}^{N}||t_n - y(\vec{x}^n)||^2

ここで\frac{1}{2} をかけるのは微分するときに具合がいいというだけで、それ以外の理由は特にないので本質的にはあってもなくても問題はありません。

また\frac{1}{N} がかけられているのも、Nの大きさにかかわらずLの大きさが同じオーダーにおさまるように大きさを調整しているだけです。

この設定した損失関数をなるべく０に近づけるというのが今回の目標となります。

学習の進め方

それでは学習の進め方を説明していきたいと思います。

パラメーターをそれぞれ動かしたときに損失関数の値がどれだけ変動するかを基にパラメーターを動かしていきます。まずパラメータを1つだけを動かしてみてどれほど損失関数が変動するかを計算する必要があります。

その計算の仕方は数学的に言うならば偏微分ということになります。

他のパラメーターを動かさず、そのパラメーターを動かした時の変化の度合いを示し、

\frac{\partial L}{\partial w_i}

のかたちで表されます。例えば、２節でのニューラルネットワークの状態だとパラメーターはw_1, w_2, w_3, b の４つで、例えばw_1 ならば

\frac{\partial L}{\partial w_1} = \frac{1}{N}\sum_{n=1}^{N}(\sigma(\vec{x}^n\cdot\vec{w}+b)-t_n)\frac{d\sigma}{dw_1}\\ = \frac{1}{N}\sum_{n=1}^{N}\{(\sigma(a_n)-t_n)\sigma(a_n)(1-\sigma(a_n))x_1\}\\ (a_n = \vec{x}^n\cdot\vec{w} + b)

右辺に関しては素直に微分すれば出てくる値ではありますが形があまりきれいにならなかったので、流し見する程度で大丈夫です。 ただ、最後にx_1 がかけられていることは覚えておいてください。バイアスにあたるbの場合だとx_1 などのような値ではなく１をかけることになります。

\frac{\partial L}{\partial b} = \frac{1}{N}\sum_{n=1}^{N}\{(\sigma(a_n)-t_n)\sigma(a_n)(1-\sigma(a_n))\}\\

パラメーターがそれぞれ\Delta w_i, \Delta b だけ変化した時、損失関数Lの変化分\Delta L は

\Delta L = \frac{\partial L}{\partial w_1}\Delta w_1 + \frac{\partial L}{\partial w_2}\Delta w_2 + \frac{\partial L}{\partial w_3}\Delta w_3 + \frac{\partial L}{\partial b}\Delta b

と表すことができます。これを見ると、\Delta L を確実に負にするためには学習率\eta(>0) を用いて

\Delta w_i = -\eta \frac{\partial L}{\partial w_i} \ \ (i = 1,2,3) \\ \Delta b = -\eta \frac{\partial L}{\partial b}

とすれば、

\Delta L = -\eta\{(\frac{\partial L}{\partial w_1})^2 + (\frac{\partial L}{\partial w_2})^2 + (\frac{\partial L}{\partial w_3})^2 + (\frac{\partial L}{\partial b})^2\} \le 0

となります。こうすると偏微分の部分がすべて２乗となるので計算した損失関数の値を減らすことができます。

参考